
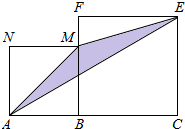
 如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为
如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为分析 根据连接BE,则BE∥AM,利用△AME的面积=△AMB的面积即可得出Sn=$\frac{1}{2}$n2,Sn-1=$\frac{1}{2}$(n-1)2=$\frac{1}{2}$n2-n+$\frac{1}{2}$,再代值计算即可得出答案.
解答 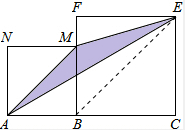 解:连接BE.
解:连接BE.
∵在线段AC同侧作正方形ABMN及正方形BCEF,
∴BE∥AM,
∴△AME与△AMB同底等高,
∴△AME的面积=△AMB的面积,
∴当AB=n时,△AME的面积记为Sn=$\frac{1}{2}$n2,
Sn-1=$\frac{1}{2}$(n-1)2=$\frac{1}{2}$n2-n+$\frac{1}{2}$,
∴当n≥2时,Sn-Sn-1=$\frac{2n-1}{2}$=$\frac{2×3-1}{2}$=$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 此题主要考查了整式的混合运算,用到的知识点是三角形面积求法以及正方形的性质,根据已知得出正确图形,得出S与n的关系是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
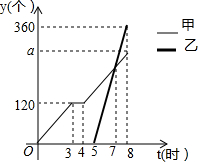 某天,甲组工人加工零件,工作中有一次停产检修机器,然后继续加工.由于任务紧急,乙组工人加入,与甲组工人一起生产零件.两组各自加工零件的数量y(个)与甲组工人加工时间t(时)之间的函数图象如图所示.
某天,甲组工人加工零件,工作中有一次停产检修机器,然后继续加工.由于任务紧急,乙组工人加入,与甲组工人一起生产零件.两组各自加工零件的数量y(个)与甲组工人加工时间t(时)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
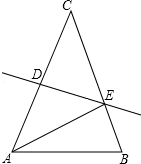 如图,在三角形纸片△ABC中,AC=BC,∠B=70°,将△ABC沿线段DE所在直线对折,使点A、点C重合,连接AE,则∠AED的度数是50度.
如图,在三角形纸片△ABC中,AC=BC,∠B=70°,将△ABC沿线段DE所在直线对折,使点A、点C重合,连接AE,则∠AED的度数是50度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
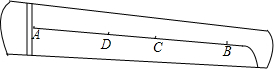 如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,求C、D之间的距离.
如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,求C、D之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
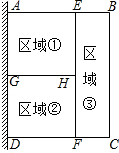 如图,某小区准备用篱笆围成一块矩形花圃ABCD,为了节省篱笆,一边利用足够长的墙,另外三边用篱笆围着,再用两段篱笆EF与GH将矩形ABCD分割成①②③三块矩形区域,而且这三块矩形区域的面积相等,现有总长80m的篱笆,当围成的花圃ABCD的面积最大时,AB的长为15m.
如图,某小区准备用篱笆围成一块矩形花圃ABCD,为了节省篱笆,一边利用足够长的墙,另外三边用篱笆围着,再用两段篱笆EF与GH将矩形ABCD分割成①②③三块矩形区域,而且这三块矩形区域的面积相等,现有总长80m的篱笆,当围成的花圃ABCD的面积最大时,AB的长为15m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com