
【题目】如图,在正方形ABCD中,E是边CD上一点(点E不与点C,D重合),连接BE.取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
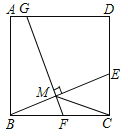
(1)求证:BE=FG.
(2)连接CM,若CM=1,试求FG的长.
【答案】(1)详见解析;(2)2.
【解析】
(1)根据正方形的性质可得AB=BC,∠ABC=∠BCD=90°,过点G作GP⊥BC,垂足为P,得矩形ABPG,进而证明△GPF≌△BCE即可得结论;
(2)根据直角三角形斜边上的中线等于斜边的一半即可得FG的长.
(1)证明:如图,
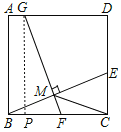
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
过点G作GP⊥BC,垂足为P,得矩形ABPG,
∴PG=AB,∠GPF=90°,
∠PGF+∠GFP=90°,
∠CBE+∠GFP=90°,
∴∠PGF=∠CBE,PG=CB,∠GPF=∠BCE=90°,
∴△GPF≌△BCE(ASA)
∴BE=FG.
(2)在Rt△BCE中,
∵点M为BE的中点,
∴BE=2CM,
∴FG=BE=2.
答:FG的长为2.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
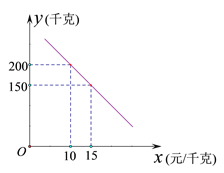
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间的函数关系如图所示.
(元/千克)之间的函数关系如图所示.
(1)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元.市场调査发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量![]() (箱)与销售价
(箱)与销售价![]() (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润![]() (元)与销售价
(元)与销售价![]() (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“早黑宝”葡萄品种是我省农科院研制的优质新品种,在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“卓黑宝”的种植面积达到196亩.
(1)求该基地这两年“早黑宝”种植面积的平均增长率;
(2)市场调查发现,当“早黑宝”的售价为20元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1750元,则售价应降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
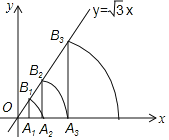
【题目】如图,直线l:y=![]() x,点A1坐标为(1,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1为半径画弧交x轴于点A2;再过点A2作x的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去.
x,点A1坐标为(1,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1为半径画弧交x轴于点A2;再过点A2作x的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去.
求:(1)点B1的坐标和∠A1OB1的度数;
(2)弦A4B3的弦心距的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com