
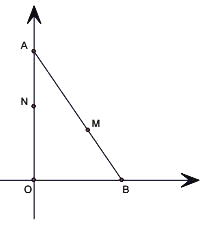
【题目】如图,己知A(0,8),B(6,0),点M、N分别是线段AB、AO上的动点,点M从点B出发,以每秒2个单位的速度向点A运动,点N从点A出发,以每秒1个单位的速度向点O运动,点M、N中有一个点停止时,另一个点也停止。设运动时间为t秒。
(1)当t为何值时,M为AB的中点;
(2)当t为何值时,△AMN为直角三角形;
(3)当t为何值时,△AMN是等腰三角形?并求此时点M的坐标.
【答案】(1)当t=![]() 秒时,M是AB的中点;(2)当
秒时,M是AB的中点;(2)当![]() 或
或![]() 时,△AMN为直角三角形;
时,△AMN为直角三角形;
(3)当![]() ,
,![]() ,
, ![]() 时,△AMN为等腰三角形,此时,M点的坐标分别是
时,△AMN为等腰三角形,此时,M点的坐标分别是![]() ,
,![]() ,
,![]() .
.
【解析】
(1)由勾股定理求出AB的长,再由中点的定义即可得出结论;
(2)运动t秒时,AN=t,BM=2t,AM=10-2t.然后分两种情况讨论:①当MN⊥AO时,△ANM∽△AOB;②当MN⊥AB时,△ANM∽△ABO;
(3)先求出M的坐标,然后分三种情况讨论:①AM=AN;②MA=MN;③NA=NM.
(1)∵A(0,8),B(6,0),∴OA=8,OB=6,∴AB=10.
∵M为AB的中点,∴MB=2t=5,∴t=![]() .
.
答:当t=![]() 秒时,M是AB的中点.
秒时,M是AB的中点.

(2)运动t秒时,AN=t,BM=2t,AM=10-2t.
①当MN⊥AO时,△ANM∽△AOB,∴![]() ,∴
,∴![]() ,∴t=
,∴t=![]() .
.
②当MN⊥AB时,△ANM∽△ABO,∴![]() ,∴
,∴![]() ,∴t=
,∴t=![]() .
.
综上:当 t=![]() 或 t=
或 t=![]() 时,△AMN为直角三角形.
时,△AMN为直角三角形.
(3)如图,过M作MC⊥OB于C,MD⊥OA于D.
∵AO⊥OB,∴∠MCB=∠AOB.
∵∠MBC=∠ABO,∴△MBC∽△ABO,∴![]() ,∴
,∴![]() ,∴MC=
,∴MC=![]() ,CB=
,CB=![]() ,∴OC=
,∴OC=![]() ,∴M(
,∴M(![]() ,
,![]() ).分三种情况讨论:
).分三种情况讨论:

①当AM=AN时,t=102t,解得:![]() ,∴M(2,
,∴M(2,![]() );
);
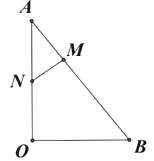
②当MA=MN时,过M作MF⊥AO,交AO于F,如图:
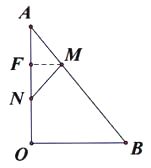
则F是AN的中点,AF=![]() ,这时,△AFM∽△AOB,∴
,这时,△AFM∽△AOB,∴![]() ,∴
,∴![]() ,解得
,解得 ![]() ,∴M(
,∴M(![]() ,
,![]() );
);
③当NA=NM时,过N作NG⊥AB,交AB于G,如图,则G是AM的中点,AG=5t.

这时,△AGN∽△AOB,∴![]() ,∴
,∴![]() ,解得:
,解得:![]() ,∴M(
,∴M(![]() ,
,![]() ).
).
综上,当 ![]() 或
或![]() 或
或![]() 时,△AMN为等腰三角形,此时,M点的坐标分别是
时,△AMN为等腰三角形,此时,M点的坐标分别是![]() .
.


科目:初中数学 来源: 题型:
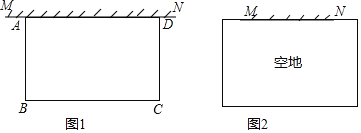
【题目】空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
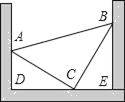
【题目】如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
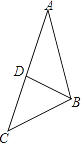
【题目】如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=ADAC;③ADBC=ABBD;④ABBC=ACBD.其中单独能够判定△ABC∽△ADB的个数是( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
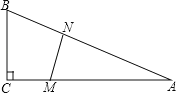
【题目】如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
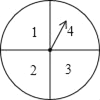
【题目】小王和小张利用如图所示的转盘做游戏,转盘的盘面被分为面积相等的4个扇形区域,且分别标有数字1,2,3,4.游戏规则如下:两人各转动转盘一次,分别记录指针停止时所对应的数字,如两次的数字都是奇数,则小王胜;如两次的数字都是偶数,则小张胜;如两次的数字是奇偶,则为平局.解答下列问题:
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程4x2+4(m﹣1)x+m2=0
(1)当m在什么范围取值时,方程有两个实数根?
(2)设方程有两个实数根x1 , x2 , 问m为何值时,x12+x22=17?
(3)若方程有两个实数根x1,x2, 问x1和x2能否同号?若能同号,请求出相应m的取值范围;若不能同号,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
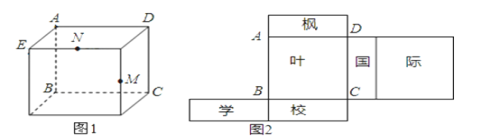
【题目】如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题:
(1)面“学”的对面是面什么?
(2)图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置; 并求出图2中△ABN的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com