
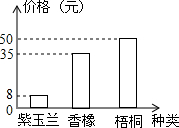
 为了响应市政府提出的“创建森林城市”的号召,市林业局计划今年在瓯江口新区种植梧桐、紫玉兰和香樟三类树苗,其中香樟树苗的株数是梧桐树苗的2倍,三种树苗的单价如图所示,设计划种植x株梧桐树苗,y株紫玉兰树苗;
为了响应市政府提出的“创建森林城市”的号召,市林业局计划今年在瓯江口新区种植梧桐、紫玉兰和香樟三类树苗,其中香樟树苗的株数是梧桐树苗的2倍,三种树苗的单价如图所示,设计划种植x株梧桐树苗,y株紫玉兰树苗;| 梧桐 | 香樟 | 紫玉兰 | 合计 | |
| 树苗株数 | x | 2x | y | 3x+y |
| 费用 | 50x | 70x | 8y | 120x+8y |
分析 (1)根据香樟树苗的株数是梧桐树苗的2倍可得香樟树2x棵,费用为35×2x=70x元,树苗的总数是三种树的和,费用是三种树的费用和;
(2)根据(1)中的合计可得$\left\{\begin{array}{l}{3x+y=150}\\{120x+8y=5040}\end{array}\right.$,再解即可;
(3)紫玉兰的价格最低,因此总费用是7232元,那么最少能种植树苗的数量就是少买紫玉兰,多买价格高的树即可.
解答 解:(1)表格:
| 梧桐 | 香樟 | 紫玉兰 | 合计 | |
| 树苗株数 | x | 2x | y | 3x+y |
| 费用 | 50x | 70x | 8y | 120x+8y |
点评 此题主要考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程组.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
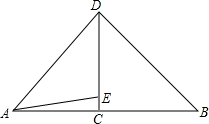 重庆市是著名的山城,许多美丽的建筑建在山上,如图,刘老师为了测量小山项一建筑物DE的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的A处测得建筑物顶端D的仰角为53°,山坡AE的坡度i=1:5,潘老师在B处测得建筑物顶端D的仰角为45°.若此时刘老师与潘老师的距离AB=200m,求建筑物DE的高度.(sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,结果精确到0.1m)
重庆市是著名的山城,许多美丽的建筑建在山上,如图,刘老师为了测量小山项一建筑物DE的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的A处测得建筑物顶端D的仰角为53°,山坡AE的坡度i=1:5,潘老师在B处测得建筑物顶端D的仰角为45°.若此时刘老师与潘老师的距离AB=200m,求建筑物DE的高度.(sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
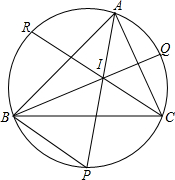 如图5,I是△ABC的内心,且∠A、∠B、∠C的平分线延长线分别交外接圆于P,Q,R点.
如图5,I是△ABC的内心,且∠A、∠B、∠C的平分线延长线分别交外接圆于P,Q,R点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com