
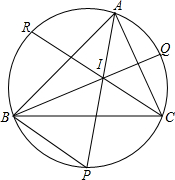
 如图5,I是△ABC的内心,且∠A、∠B、∠C的平分线延长线分别交外接圆于P,Q,R点.
如图5,I是△ABC的内心,且∠A、∠B、∠C的平分线延长线分别交外接圆于P,Q,R点.分析 (1)根据同弧所对的圆周角等于圆心角的一半,即可求解.
(2)根据角平分线的性质,同弧所对的圆周角相等,得到角与角的数量关系,证得角相等,由等角对等边得到结论.
(3)根据同圆或等圆中等弧所对的弦相等,大弧对的弦也大,推出结论.
解答 解:(1)∵若$\widehat{BPC}$所对的圆心角为140°,
∴∠BAC=$\frac{1}{2}$×140°=70°,
∵AP平分∠BAC,
∴∠BAP=$\frac{1}{2}$∠BAC=35°;
(2)相等
∵AP平分∠BAC,BQ平分∠ABC,
∴∠BIP=∠BAP+∠ABI=$\frac{1}{2}$(∠BAC+∠ABC),
∠IBP=∠IBC+∠PBC,
∵∠PBC=∠PAC=$\frac{1}{2}$∠BAC,
∴∠IBP=$\frac{1}{2}$(∠BAC+∠ABC),
∴∠BIP=∠IBP,
∴BP=PI;
(3)∵$\widehat{ABP}$$>\widehat{AB}$,
∴AP>AB,①
∵$\widehat{CAR}$$>\widehat{AC}$,
∴CR>AC,②
∵$\widehat{BCQ}$$>\widehat{BC}$,
∴BQ>BC,③
∴①+②+③得:
∴AP+BQ+CR>BC+CA+AB.
点评 本题考查了三角形的内切圆和内心的,以及等腰三角形的判定与性质,同弧所对的圆周角相等.正确的识别同弧所对的圆周角是解题的关键.


科目:初中数学 来源: 题型:解答题
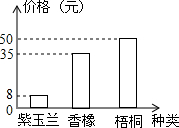 为了响应市政府提出的“创建森林城市”的号召,市林业局计划今年在瓯江口新区种植梧桐、紫玉兰和香樟三类树苗,其中香樟树苗的株数是梧桐树苗的2倍,三种树苗的单价如图所示,设计划种植x株梧桐树苗,y株紫玉兰树苗;
为了响应市政府提出的“创建森林城市”的号召,市林业局计划今年在瓯江口新区种植梧桐、紫玉兰和香樟三类树苗,其中香樟树苗的株数是梧桐树苗的2倍,三种树苗的单价如图所示,设计划种植x株梧桐树苗,y株紫玉兰树苗;| 梧桐 | 香樟 | 紫玉兰 | 合计 | |
| 树苗株数 | x | 2x | y | 3x+y |
| 费用 | 50x | 70x | 8y | 120x+8y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
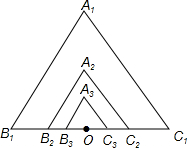 如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn.C2,C3,…,Cn都在B1C1边上.
如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn.C2,C3,…,Cn都在B1C1边上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
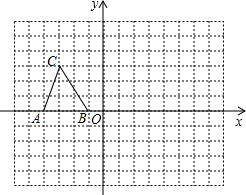 如图,在平面直角坐标系中(网格正方形的边长为1个单位),已知△ABC三个顶点的坐标分别为A(-4,0),B(-1,0),C(-3,3).
如图,在平面直角坐标系中(网格正方形的边长为1个单位),已知△ABC三个顶点的坐标分别为A(-4,0),B(-1,0),C(-3,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
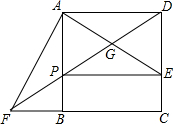 如图,在正方形ABCD中,点E时CD边上一点,AF⊥AE交CB的延长线于点F,连接DF分别交于AE、AB于点C、P连接PE.
如图,在正方形ABCD中,点E时CD边上一点,AF⊥AE交CB的延长线于点F,连接DF分别交于AE、AB于点C、P连接PE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com