
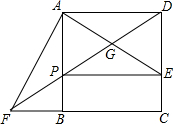
 如图,在正方形ABCD中,点E时CD边上一点,AF⊥AE交CB的延长线于点F,连接DF分别交于AE、AB于点C、P连接PE.
如图,在正方形ABCD中,点E时CD边上一点,AF⊥AE交CB的延长线于点F,连接DF分别交于AE、AB于点C、P连接PE.分析 (1)若要证明AE=AF,则可证明以上两条线段所在的三角形△ADE≌△ABF全等即可;
(2)证得△ADP∽△PBF,设DE=x,利用相似的性质得出方程求得方程的解即可.
解答 证明:(1)∵四边形ABCD是正方形,
∴∠ADE=∠ABC=∠DAB=90°,AD=AB,AD∥BC,AB∥CD,
∵AF⊥AE,
∴∠EAF=90°,
∴∠DAE=∠BAF,
在△ADE和△ABF中,
$\left\{\begin{array}{l}{∠DAE=∠BAF}\\{AD=AB}\\{∠ADE=∠ABF}\end{array}\right.$,
∴△ADE≌△ABF(ASA),
∴AF=AE;
(2)∵△ADE≌△ABF,
∴DE=BF,
∵四边形APED是矩形,
∴DE=AP,
∴DE=AP=BF,
设DE=x,则AP=BF=x,
∵AD∥BF,
∴△ADP∽△PBF,
∴$\frac{AD}{FB}$=$\frac{AP}{PB}$,
即$\frac{2}{x}$=$\frac{x}{2-x}$,
解得:x=$\sqrt{5}$-1或x=-$\sqrt{5}$-1(不合题意,舍去)
∴当DE=$\sqrt{5}$-1时,四边形APED是矩形.
点评 此题考查正方形的性质,三角形全等的判定与性质,相似三角形的判定与性质,矩形的性质,利用相似建立方程是解决问题的关键.


科目:初中数学 来源: 题型:解答题
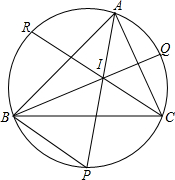 如图5,I是△ABC的内心,且∠A、∠B、∠C的平分线延长线分别交外接圆于P,Q,R点.
如图5,I是△ABC的内心,且∠A、∠B、∠C的平分线延长线分别交外接圆于P,Q,R点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查市场上酸奶的质量情况 | |
| B. | 调查某品牌圆珠笔芯的使用寿命 | |
| C. | 调查乘坐飞机的旅客是否携带了违禁物品 | |
| D. | 调查我市市民收看晚间新闻的情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com