
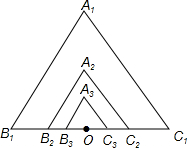
 如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn.C2,C3,…,Cn都在B1C1边上.
如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn.C2,C3,…,Cn都在B1C1边上.分析 (1)由于点O是B1C1中点,A2是OA1的中点,则可得到正△A2B2C2的边长为$\frac{1}{2}$,正△A3B3C3的边长为($\frac{1}{2}$)2,利用此规律可得第n个三角形△AnBnCn(n≥2)的边长为($\frac{1}{2}$)n-1,所以正△A10B10C10的边长为($\frac{1}{2}$)9,正△A7B7C7的边长为($\frac{1}{2}$)6,然后根据对应边的比等于相似比即可得到△A10B10C10和△A7B7C7的相似比,再根据位似的定义确定位似中心;
(2)利用第n个三角形△AnBnCn(n≥2)的边长为($\frac{1}{2}$)n-1易得第n个三角形△AnBnCn(n≥2)的周长.
解答 解:(1)∵△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,
∴正△A2B2C2的边长为$\frac{1}{2}$,
正△A3B3C3的边长为($\frac{1}{2}$)2,
正△A10B10C10和的边长为($\frac{1}{2}$)9,正△A7B7C7的边长为($\frac{1}{2}$)6,
∴正△A10B10C10和正△A7B7C7的相似比=$\frac{(\frac{1}{2})^{9}}{(\frac{1}{2})^{6}}$=$\frac{1}{8}$;它们的位似中心为点O;
(2)∵第n个三角形△AnBnCn(n≥2)的边长为($\frac{1}{2}$)n-1,
∴第n个三角形△AnBnCn(n≥2)的周长为$\frac{3}{{2}^{n-1}}$.
点评 本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.注意:①两个图形必须是相似形;②对应点的连线都经过同一点;③对应边平行.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
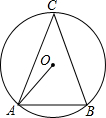 如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
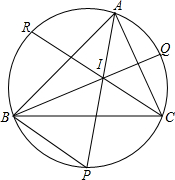 如图5,I是△ABC的内心,且∠A、∠B、∠C的平分线延长线分别交外接圆于P,Q,R点.
如图5,I是△ABC的内心,且∠A、∠B、∠C的平分线延长线分别交外接圆于P,Q,R点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2cm | B. | $\frac{4}{3}$cm | C. | 2$\sqrt{3}$cm | D. | $\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查市场上酸奶的质量情况 | |
| B. | 调查某品牌圆珠笔芯的使用寿命 | |
| C. | 调查乘坐飞机的旅客是否携带了违禁物品 | |
| D. | 调查我市市民收看晚间新闻的情况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com