
分析 (1)每辆A型车和B型车的售价分别是x万元、y万元.则等量关系为:1辆A型车和3辆B型车,销售额为96万元,2辆A型车和1辆B型车,销售额为62万元;
(2)设采购A型车为a辆,则采购B型车的数量为(20-a)辆,然后根据数量和单价列出不等式组,求解得到a的取值范围,再根据a是正整数确定进货方案.
解答 解:(1)每辆A型车和B型车的售价分别是x万元、y万元.则
$\left\{\begin{array}{l}{x+3y=96}\\{2x+y=62}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{x=18}\\{y=26}\end{array}\right.$.
答:每辆A型车的售价为18万元,每辆B型车的售价为26万元;
(2)设采购A型车为a辆,则采购B型车的数量为(20-a)辆,由题意得,$\left\{\begin{array}{l}{20-a≥\frac{7}{9}a①}\\{-0.6a+26≥20②}\end{array}\right.$,
解不等式①得,a≥11,
解不等式②得,a≤15,
所以,不等式组的解集是11≤a≤15,
∵a为正整数,
∴a可取的值为11、12、13、14、15,
所以,该商家共有5种进货方案.
点评 本题考查了一元一次不等式组的应用和二元一次方程组的应用.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
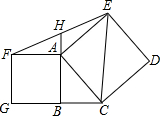 已知:如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向△ABC外作正方形ACDE和正方形ABGF,连接EF、EC,延长BA交EF于H.
已知:如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向△ABC外作正方形ACDE和正方形ABGF,连接EF、EC,延长BA交EF于H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
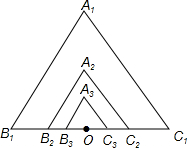 如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn.C2,C3,…,Cn都在B1C1边上.
如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn.C2,C3,…,Cn都在B1C1边上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 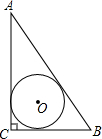 | B. | 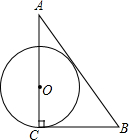 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
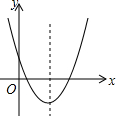 二次函数的图象如图所示,其对称轴为x=$\frac{3}{2}$,A(2,y1),B($\frac{4}{3}$,y2)两点均在二次函数的图象上,则y1与y2的大小关系为y1>y2.
二次函数的图象如图所示,其对称轴为x=$\frac{3}{2}$,A(2,y1),B($\frac{4}{3}$,y2)两点均在二次函数的图象上,则y1与y2的大小关系为y1>y2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com