
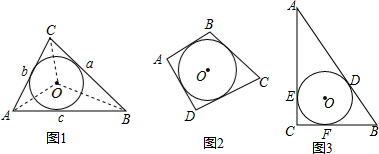
分析 (1)已知已给出示例,我们仿照例子,连接OA,OB,OC,OD,则四边形被分为四个小三角形,且每个三角形都以内切圆半径为高,以四边形各边作底,这与题目情形类似.仿照证明过程,r易得.
(2)如图3,连接OE、OF,则四边形OECF是正方形,OE=EC=CF=FO=r,解直角三角形求得结果.
解答 解:(1)如图2,连接OA、OB、OC、OD.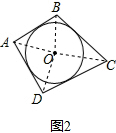
∵S=S△AOB+S△BOC+S△COD+S△AOD=$\frac{1}{2}$ar$+\frac{1}{2}$br$+\frac{1}{2}$cr$+\frac{1}{2}$dr=$\frac{1}{2}$(+b+c+d)r,
∴r=$\frac{2S}{a+b+c+d}$;
(2)如图3连接OE、OF,则四边形OECF是正方形,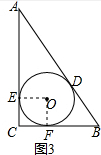
OE=EC=CF=FO=r,
在Rt△ABC中,AC2+BC2=AB2,
(3+r)2+(2+r)2=52,
r2+5r-6=0,
解得:r=1.
点评 本题考查了学生的学习、理解、创新新知识的能力,同时考查了解直角三角形及等腰梯形等相关知识.这类创新性题目已经成为新课标热衷的考点,是一道值得练习的基础题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
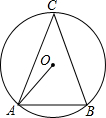 如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
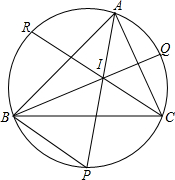 如图5,I是△ABC的内心,且∠A、∠B、∠C的平分线延长线分别交外接圆于P,Q,R点.
如图5,I是△ABC的内心,且∠A、∠B、∠C的平分线延长线分别交外接圆于P,Q,R点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com