
分析 根据题意画出相应的图形,如图所示,由两直角边的长,利用勾股定理求出斜边AC的长,由圆O为三角形的内切圆,得到三角形三边与圆O相切,切点分别为D,E,F,连接圆心与各个切点,根据切线的性质得到OD与AB垂直,OF与BC垂直,又∠B为直角,可得四边形ODBF为矩形,又两半径OD=OF,可得此矩形为正方形,根据正方形的性质得到四条边相等,设出圆的半径为r,根据AD与AE为圆的两条切线,根据切线长定理得到AD=AE=12-r,同理可得出CE=CF=5-r,进而得到AC=AE+EC=AD+CF,列出关于r的方程,求出方程的解可得出r的值.
解答  解:∵直角三角形的两直角边长BC=5cm,AC=12cm,
解:∵直角三角形的两直角边长BC=5cm,AC=12cm,
∴根据勾股定理得到直角三角形的斜边AC=$\sqrt{{5}^{2}{+12}^{2}}$=13cm,
又圆O为三角形的内切圆,D,E,F分别为切点,连接OD,OE,OF,
∴OD⊥AB,OF⊥BC,
∴∠ODB=∠B=∠OFB=90°,
∴四边形OFBD为矩形,又OD=OF,
∴四边形OFBD为正方形,
∴OD=DB=BF=OF,
又AD,AE为圆O的两条切线,
∴AD=AE,
同理CE=CF,BD=BF,
设圆O的半径为rcm,则有BD=BF=rcm,
∴CF=CE=(5-r)cm,AD=AE=(12-r)cm,
又AC=AE+EC=AD+CF=12-r+5-r=17-2r=13,
解得:r=2,
则该直角三角形的内切圆的半径为2cm.
故答案为:2.
点评 此题考查了三角形的内切圆与内心,涉及的知识有:勾股定理,正方形的判定与性质,切线长定理,利用了方程及转化的思想,本题的关键是根据题意画出相应的图形,添加合适的辅助线,设出未知数,建立方程来解决问题.


科目:初中数学 来源: 题型:解答题
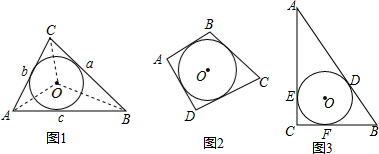
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
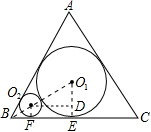 如图,在边长为54$\sqrt{3}$的正三角形ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB、BC相切;圆O3与圆O2外切,且与AB、BC相切…如此继续下去,请计算圆O5的周长为$\frac{2}{3}$π.(结果保留π)
如图,在边长为54$\sqrt{3}$的正三角形ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB、BC相切;圆O3与圆O2外切,且与AB、BC相切…如此继续下去,请计算圆O5的周长为$\frac{2}{3}$π.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
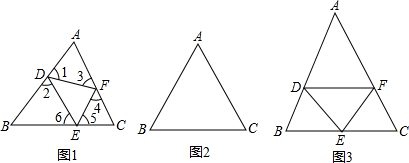
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
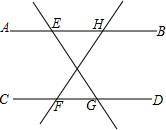 如图,下列条件中,不能判断直线AB∥CD的是( )
如图,下列条件中,不能判断直线AB∥CD的是( )| A. | ∠HEG=∠EGF | B. | ∠EHF+∠CFH=180° | C. | ∠EHF=∠CFH | D. | ∠AEG=∠DGE |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{20}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{2000}$ | D. | $\sqrt{200}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com