
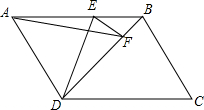
 如图,在平行四边形ABCD中,AD⊥BD,点E、点F分别在AB、BD上,且AD=AE=DF,连接DE、AF、EF.
如图,在平行四边形ABCD中,AD⊥BD,点E、点F分别在AB、BD上,且AD=AE=DF,连接DE、AF、EF.分析 (1)根据等腰直角三角形的性质和平行四边形的性质即可得到结果.
(2)过A作AG⊥DE于G构造全等三角形,根据等腰三角形的性质得到DE=2DG,通过证明△ADG≌△EDF,即可得到结论.
解答 解:(1)∵AD⊥BD,
∴∠ADB=90°,
∵AD=DF,
∴∠DAF=45°,
∵∠EAF=15°,
∴∠BAD=60°,
∴∠ABD=30°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BDC=∠ABD=30°;
(2)如图,过A作AG⊥DE于G,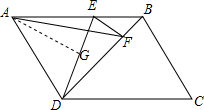
∴∠AGD=90°,
∵AD=AE,
∴DE=2DG,
∵DE⊥EF,
∴∠DEF=90°,
∴∠DAG+∠ADG=∠ADG+∠EDF=90°,
∴∠DAG=∠EDF,
在△ADG与△EDF中,
$\left\{\begin{array}{l}{∠AGD=∠DEF}\\{∠DAG=∠EDF}\\{AD=DF}\end{array}\right.$,
∴△ADG≌△EDF,
∴DG=EF,
∴DE=2EF.
点评 本题考查了平行四边形的性质,全等三角形的判定和性质,等腰直角三角形的性质,作辅助线构造全等三角形是解题的关键.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:解答题
| x | 30 | 32 | 34 | 36 |
| y | 40 | 36 | 32 | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
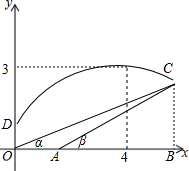 某防空部队进行射击训练,在地面上设有O、A两个观测点,测得空中固定目标C的仰角分别为α、β,OA=1千米,已知tanα=$\frac{9}{28}$,tanβ=$\frac{3}{8}$.一直升飞机在O点正上方$\frac{5}{3}$千米D点处,向目标C发射防空导弹,导弹飞行的轨道近似为抛物线,当导弹飞行到距O点水平距离4千米时,达到最大高度3千米.建立如图所示的平面直角坐标系.
某防空部队进行射击训练,在地面上设有O、A两个观测点,测得空中固定目标C的仰角分别为α、β,OA=1千米,已知tanα=$\frac{9}{28}$,tanβ=$\frac{3}{8}$.一直升飞机在O点正上方$\frac{5}{3}$千米D点处,向目标C发射防空导弹,导弹飞行的轨道近似为抛物线,当导弹飞行到距O点水平距离4千米时,达到最大高度3千米.建立如图所示的平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上.若AM:MB=AN:ND=1:2,则tan∠MCN=$\frac{3\sqrt{3}}{13}$.
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上.若AM:MB=AN:ND=1:2,则tan∠MCN=$\frac{3\sqrt{3}}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
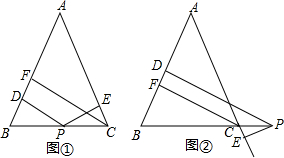 如图1,在△ABC中,AB=AC,在BC边上有任意一点P,则点P到AB,AC的距离之和等于AB边上的高,即PD+PE=CF,如图2,如果点P在BC的延长线上,那么请猜想点P到AB,AC的距离与AB边上的高的关系.(提示:用面积法)
如图1,在△ABC中,AB=AC,在BC边上有任意一点P,则点P到AB,AC的距离之和等于AB边上的高,即PD+PE=CF,如图2,如果点P在BC的延长线上,那么请猜想点P到AB,AC的距离与AB边上的高的关系.(提示:用面积法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com