练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（1）在直角三角形中，有一个锐角是另一个锐角的2倍，则较小的锐角为__________．

    （2）在中，，，CD平分，点D，E分别在AB，AC上，且，则__________．

    【答案】

    【解析】

    （1）较小的锐角为x，根据直角三角形的两锐角互余列式计算，即可得到答案；

    （2）首先利用三角形内角和定理得出∠ACB的度数，再利用平行线的性质以及角平分线的定义分析得出答案．

    （1）设较小的锐角为x，则较大的锐角为2x，

    则x+2x=90°，

    解得：x=30°．

    （2）∵∠A=62°，∠B=74°，

    ∴∠ACB=180°﹣62°﹣74°=44°．

    ∵CD平分∠ACB，

    ∴∠ACD=∠DCB=22°．

    ∵DE∥BC，

    ∴∠EDC=∠DCB=22°．

    故答案为：30°，22°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形纸片ABCD沿其对角线AC折叠，使点B落在点B′的位置，AB′与CD交于点E．

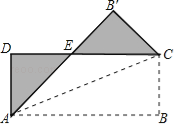
    （1）求证：△AED≌△CEB′；

    （2）求证：点E在线段AC的垂直平分线上；

    （3）若AB=8，AD=3，求图中阴影部分的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了提高服务质量，某宾馆决定对甲、乙两种套房进行星级提升，已知甲种套房提升费用比乙种套房提升费用少3万元，如果提升相同数量的套房，甲种套房费用为625万元，乙种套房费用为700万元．

    （1）甲、乙两种套房每套提升费用各多少万元？

    （2）如果需要甲、乙两种套房共80套，市政府筹资金不少于2090万元，但不超过2096万元，且所筹资金全部用于甲、乙种套房星级提升，市政府对两种套房的提升有几种方案？哪一种方案的提升费用最少？

    （3）在（2）的条件下，根据市场调查，每套乙种套房的提升费用不会改变，每套甲种套房提升费用将会提高a万元（a＞0），市政府如何确定方案才能使费用最少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】7张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（ ）

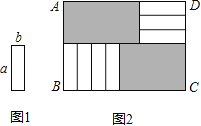
    A.a=bB.a=3bC.a=bD.a=4b

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB=6，BC=4，过对角线BD中点O的直线分别交AB，CD边于点E，F．

    （1）求证：四边形BEDF是平行四边形；

    （2）当四边形BEDF是菱形时，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某学校教学楼AB的后面有一建筑物CD，在距离CD正后方28米的观测点P处，以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A，而在建筑物CD上距离地面2米高的E处，测得教学楼的顶端A的仰角为45°，求教学楼AB的高度（结果保留整数）．

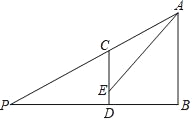
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知抛物线y=﹣x2+bx+c交y轴于点A（0，4），交x轴于点B（4，0），点P是抛物线上一动点，过点P作x轴的垂线PQ，过点A作AQ⊥PQ于点Q，连接AP．

    （1）填空：抛物线的解析式为　 　，点C的坐标　 　；

    （2）点P在抛物线上运动，若△AQP∽△AOC，求点P的坐标；

    （3）如图2，当点P位于抛物线的对称轴的右侧，若将△APQ沿AP对折，点Q的对应点为点Q'，请直接写出当点Q'落在坐标轴上时点P的坐标．

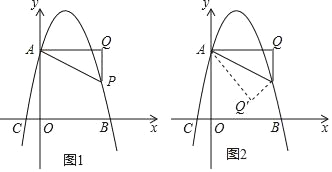
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形OABC放在平面直角坐标系中，O为原点，点A在x轴的正半轴上，B（8，6），点D是射线AO上的一点，把△BAD沿直线BD折叠，点A的对应点为A′．

    （Ⅰ）若点A′落在矩形的对角线OB上时，OA′的长=　 　；

    （Ⅱ）若点A′落在边AB的垂直平分线上时，求点D的坐标；

    （Ⅲ）若点A′落在边AO的垂直平分线上时，求点D的坐标（直接写出结果即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为了美化环境，计划在一定的时间内完成绿化面积万亩的任务，后来市政府调整了原定计划，不但绿化面积要在原计划的基础上增加，而且要提前年完成任务，经测算要完成新的计划，平均每年的绿化面积必须比原计划多万亩，求原计划平均每年的绿化面积．

    查看答案和解析>>

    同步练习册答案