
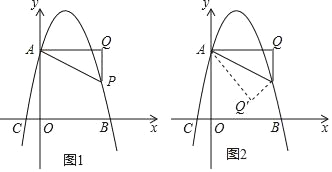
【题目】如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作AQ⊥PQ于点Q,连接AP.
(1)填空:抛物线的解析式为 ,点C的坐标 ;
(2)点P在抛物线上运动,若△AQP∽△AOC,求点P的坐标;
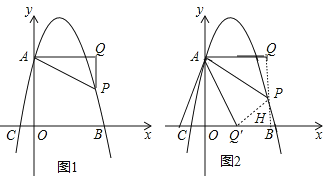
(3)如图2,当点P位于抛物线的对称轴的右侧,若将△APQ沿AP对折,点Q的对应点为点Q',请直接写出当点Q'落在坐标轴上时点P的坐标.
【答案】(1)y=﹣x2+3x+4;(﹣1,0);(2)点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)点P的坐标为(4,0)或(5,﹣6)或(2,6)
);(3)点P的坐标为(4,0)或(5,﹣6)或(2,6)
【解析】分析:(1)利用待定系数法求抛物线解析式,然后利用抛物线解析式得到一元二次方程,通过解一元二次方程得到C点坐标;
(2)利用△AQP∽△AOC得到AQ=4PQ,设P(m,﹣m2+3m+4),所以m=4|4﹣(﹣m2+3m+4|,然后解方程4(m2﹣3m)=m和方程4(m2﹣3m)=﹣m得P点坐标;
(3)设P(m,﹣m2+3m+4)(m>![]() ),当点Q′落在x轴上,延长QP交x轴于H,如图2,则PQ=m2﹣3m,证明Rt△AOQ′∽Rt△Q′HP,利用相似比得到Q′B=4m﹣12,则OQ′=12﹣3m.在Rt△AOQ′中,利用勾股定理得到方程42+(12﹣3m)2=m2,然后解方程求出m得到此时P点坐标;当点Q′落在y轴上,易得点A、Q′、P、Q所组成的四边形为正方形,利用PQ=PQ′得到|m2﹣3m|=m,然后解方程m2﹣3m=m和方程m2﹣3m=﹣m得此时P点坐标.
),当点Q′落在x轴上,延长QP交x轴于H,如图2,则PQ=m2﹣3m,证明Rt△AOQ′∽Rt△Q′HP,利用相似比得到Q′B=4m﹣12,则OQ′=12﹣3m.在Rt△AOQ′中,利用勾股定理得到方程42+(12﹣3m)2=m2,然后解方程求出m得到此时P点坐标;当点Q′落在y轴上,易得点A、Q′、P、Q所组成的四边形为正方形,利用PQ=PQ′得到|m2﹣3m|=m,然后解方程m2﹣3m=m和方程m2﹣3m=﹣m得此时P点坐标.
详解:(1)把A(0,4),B(4,0)分别代入y=﹣x2+bx+c得:
![]() ,
,
解得:![]() ,∴抛物线解析式为y=﹣x2+3x+4,
,∴抛物线解析式为y=﹣x2+3x+4,
当y=0时,﹣x2+3x+4=0,解得:x1=﹣1,x2=4,∴C(﹣1,0);
故答案为:y=﹣x2+3x+4;(﹣1,0);
(2)∵△AQP∽△AOC,∴![]() =
=![]() =
=![]() ==4,即AQ=4PQ.
==4,即AQ=4PQ.
设P(m,﹣m2+3m+4),∴m=4|4﹣(﹣m2+3m+4|,
即4|m2﹣3m|=m,解方程4(m2﹣3m)=m得:m1=0(舍去),m2=![]() ,
,
此时P点坐标为(![]() );
);
解方程4(m2﹣3m)=﹣m得:m1=0(舍去),m2=![]() ,
,
此时P点坐标为(![]() );
);
综上所述:点P的坐标为(![]() )或(
)或(![]() );
);
(3)设P(m,﹣m2+3m+4)(m>![]() ),
),
当点Q′落在x轴上,延长QP交x轴于H,如图2,
则PQ=4﹣(﹣m2+3m+4)=m2﹣3m.
∵△APQ沿AP对折,点Q的对应点为点Q',
∴∠AQ′P=∠AQP=90°,AQ′=AQ=m,PQ′=PQ=m2﹣3m.
∵∠AQ′O=∠Q′PH,∴Rt△AOQ′∽Rt△Q′HP,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得:Q′B=4m﹣12,
,解得:Q′B=4m﹣12,
∴OQ′=m﹣(4m﹣12)=12﹣3m.
在Rt△AOQ′中,42+(12﹣3m)2=m2,
整理得:m2﹣9m+20=0,解得:m1=4,m2=5,
此时P点坐标为(4,0)或(5,﹣6);
当点Q′落在y轴上,则点A、Q′、P、Q所组成的四边形为正方形,
∴PQ=PQ′,即|m2﹣3m|=m,解方程m2﹣3m=m得:m1=0(舍去),m2=4,
此时P点坐标为(4,0);
解方程m2﹣3m=﹣m得:m1=0(舍去),m2=2,此时P点坐标为(2,6).
综上所述:点P的坐标为(4,0)或(5,﹣6)或(2,6)


科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵5元,用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)若商店计划购买这两种商品共40件,且投入的经费不超过1150元,那么,最多可购买多少件甲种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对四边形ABCD添加以下条件,使之成为平行四边形,正面的添加不正确的是( )
A. AB∥CD,AD=BCB. AB=CD,AB∥CD
C. AB=CD,AD=BCD. AC与BD互相平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在直角三角形中,有一个锐角是另一个锐角的2倍,则较小的锐角为__________.
(2)在![]() 中,
中,![]() ,
,![]() ,CD平分
,CD平分![]() ,点D,E分别在AB,AC上,且
,点D,E分别在AB,AC上,且![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现有甲、乙两家商店出售两种同样的笔记本和钢笔.他们的定价相同:笔记本定价为每本25元,钢笔每支定价6元,但是他们的优惠方案不同,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.已知七年级需笔记本20本,钢笔x支(大于20支).问:
(1)在甲店购买需付款 元,在乙店购买需付款 元;
(2)若x=30,通过计算说明此时到哪家商店购买较为合算?
(3)当x=40时,请设计一种方案,使购买最省钱?算出此时需要付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具.利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a-b|,若a>b,则可简化为AB=a-b;线段AB的中点M表示的数为![]() .
.
(问题情境)
已知数轴上有A、B两点,分别表示的数为-10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
![]()
(综合运用)
(1)运动开始前,A、B两点的距离为______;线段AB的中点M所表示的数______.
(2)点A运动t秒后所在位置的点表示的数为______;点B运动t秒后所在位置的点表示的数为______;(用含t的式子表示)
(3)它们按上述方式运动,A、B两点经过多少秒会相距4个单位长度?
(4)若A,B按上述方式运动,直接写出中点M的运动方向和运动速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两座建筑物的水平距离BC为40m,从D点测得A点的仰角为30°,B点的俯角为10°,求建筑物AB的高度(结果保留小数点后一位).
参考数据sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,![]() 取1.732.
取1.732.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形 A BCD 中,对角线 A C、BD 相交于点 O,DE 平分∠A DO 交 AC 于点 E ,把 ![]() A DE 沿AD 翻折,得到
A DE 沿AD 翻折,得到![]() A DE’,点 F 是 DE 的中点,连接 A F、BF、E’F,若 AE=
A DE’,点 F 是 DE 的中点,连接 A F、BF、E’F,若 AE=![]() .
.
下列结论 :①AD 垂直平分 EE’,② tan∠ADE =![]() -1,
-1,
③ C![]() A DE - C
A DE - C![]() ODE =2
ODE =2![]() -1, ④ S四边形AEFE=
-1, ④ S四边形AEFE= ![]()
其中结论正确的个数是 ( ) .

A. 4 个 B. 3 个 C. 2 个 D. 1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中, AD// BC, ∠B=90°, AD=2, BC=5,E是AB上一点,将△BCE沿着直线CE翻折,点B恰好与点D重合,则BE=__

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com