练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，梯形ABCD中, AD// BC, ∠B=90°, AD=2, BC=5,E是AB上一点，将△BCE沿着直线CE翻折,点B恰好与点D重合,则BE=__

    【答案】

    【解析】

    如图作DM⊥BC于M，先证明四边形ABMD是矩形，在Rt△DMC中求出DM，再在Rt△AED中利用勾股定理即可解决问题．

    解：如图，作DM⊥BC于M．

    ∵∠A＝∠B＝∠DMB＝90°，

    ∴四边形ABMD是矩形，

    ∴AD＝BM＝2，AB＝DM，

    ∵点B恰好与点D重合，

    ∵BC＝CD＝5，

    在Rt△DMC中，CM＝BCBM＝3，CD＝5，

    ∴DM＝AB＝＝4，

    设BE＝DE＝x，

    在Rt△AED中，∵AE2＋AD2＝ED2，

    ∴（4x）2＋22＝x2，

    解得x＝，即BE＝，

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

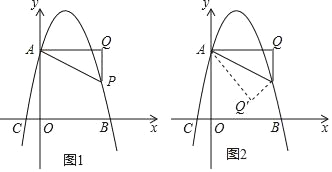
    【题目】如图1，已知抛物线y=﹣x2+bx+c交y轴于点A（0，4），交x轴于点B（4，0），点P是抛物线上一动点，过点P作x轴的垂线PQ，过点A作AQ⊥PQ于点Q，连接AP．

    （1）填空：抛物线的解析式为　 　，点C的坐标　 　；

    （2）点P在抛物线上运动，若△AQP∽△AOC，求点P的坐标；

    （3）如图2，当点P位于抛物线的对称轴的右侧，若将△APQ沿AP对折，点Q的对应点为点Q'，请直接写出当点Q'落在坐标轴上时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，点D，E分别在AC，AB上，且AD＝AE，点O是BD和CE的交点，则：①△ABD≌△ACE；②△BOE≌△COD；③点O在∠BAC的平分线上，以上结论(　　)

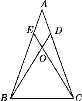
    A.都正确B.都不正确

    C.只有一个正确D.只有一个不正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为了美化环境，计划在一定的时间内完成绿化面积万亩的任务，后来市政府调整了原定计划，不但绿化面积要在原计划的基础上增加，而且要提前年完成任务，经测算要完成新的计划，平均每年的绿化面积必须比原计划多万亩，求原计划平均每年的绿化面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，，点E在CD上，EM和EN三等分，．①若，则__________；②当__________时，．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知四边形ABCD中,点E是CD上的点(不与CD的中点重合), DE=AB, ∠BAC=∠D，AD=AC

    (1)求证:四边形AECB是等腰梯形；

    (2)点F 是AB 边延长线上一点，且BC=CF .联结CF、EF,若AC⊥EF求证：四边形AECF是菱形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，的半径，AB是弦，直线EF经过点B，于点C，．

    求证：EF是的切线；

    若，求AB的长；

    在的条件下，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】单位组织员工自驾游，并打算在一家租车公司租用同一品牌同款的5座或7座越野车组成一个车队．该租车公司同品牌同款的7座越野车的日租金比5座的多300元．已知该单位参加自驾游的员工共有40人，其中10人可以担任司机，但这10人中至少需要留出3人做为机动司机，以备轮换替代．

    （1）有人建议租8辆5座的越野车，刚好可以载40人．他的建议合理吗？请说明理由；

    （2）请为该单位设计一种租车方案，使车队租车的日租金最少，并说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在直角坐标系中,点A在x轴上,且A(4,0),点B在y轴上，且B(0,4).

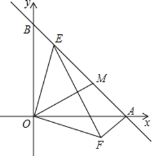
    (1)求线段AB的长；

    (2)若点E在线段AB上,OE⊥OF,且OE=OF,求AE+AF的值；

    (3)在（2）的条件下，过O作OM⊥EF,交AB于M,试确定线段BE、EM、AM之间的数量关系?并证明你的结论.

    查看答案和解析>>

    同步练习册答案