
【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )
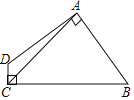
A. 15 B. 12.5 C. 14.5 D. 17
【答案】B
【解析】过A作AE⊥AC,交CB的延长线于E,判定△ACD≌△AEB,即可得到△ACE是等腰直角三角形,四边形ABCD的面积与△ACE的面积相等,根据S△ACE=![]() ×5×5=12.5,即可得出结论.
×5×5=12.5,即可得出结论.
如图,过A作AE⊥AC,交CB的延长线于E,
∵∠DAB=∠DCB=90°,
∴∠D+∠ABC=180°=∠ABE+∠ABC,
∴∠D=∠ABE,
又∵∠DAB=∠CAE=90°,
∴∠CAD=∠EAB,
又∵AD=AB,
∴△ACD≌△AEB,
∴AC=AE,即△ACE是等腰直角三角形,
∴四边形ABCD的面积与△ACE的面积相等,
∵S△ACE=![]() ×5×5=12.5,
×5×5=12.5,
∴四边形ABCD的面积为12.5,
故选B.


科目:初中数学 来源: 题型:
【题目】如图1,将长为10的线段OA绕点O旋转90°得到OB,点A的运动轨迹为![]() ,P是半径OB上一动点,Q是
,P是半径OB上一动点,Q是![]() 上的一动点,连接PQ.
上的一动点,连接PQ.
发现:∠POQ=________时,PQ有最大值,最大值为________;
思考:(1)如图2,若P是OB中点,且QP⊥OB于点P,求![]() 的长;
的长;
(2)如图3,将扇形AOB沿折痕AP折叠,使点B的对应点B′恰好落在OA的延长线上,求阴影部分面积;
探究:如图4,将扇形OAB沿PQ折叠,使折叠后的弧QB′恰好与半径OA相切,切点为C,若OP=6,求点O到折痕PQ的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
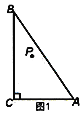
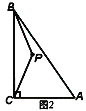
【题目】如图1.在△ABC中,∠ACB=90°,点P为△ABC内一点.
(1)连接PB、PC,将△BCP沿射线CA方向平移,得到△DAE,点B、C、P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,AB+BP=9,CE=![]() ,求AB的长.
,求AB的长.
(2)如图3,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=4,AB=8时,根据此图求PA+PB+PC的最小值.
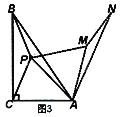
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,AB=AC,点D是斜边BC的中点,点E、F分别是AB、AC边上的点,且DE⊥DF.
(1)证明:BE+CF=EF2;
(2)若BE=12,CF=5,求△DEF的面积.
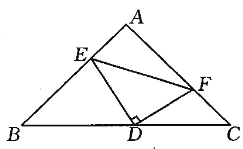
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“数形结合"是一种重要的数学思想,观察下面的图形和算式.
![]()
![]()
![]()
![]()
解答下列问题:
(1)试猜想1+3+5+7+9+…+19=______=( );
(2)试猜想,当n是正整数时,1+3+5+7+9+…+(2n-1)= ;
(3)请用(2)中得到的规律计算:19+21+23+25+27+…+99.
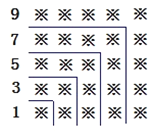
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为线段
为线段![]() 上一动点,分别过点
上一动点,分别过点![]() 作
作![]() ,
,![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的值;
的值;
(2)探究:当点![]() 满足什么条件时,
满足什么条件时,![]() 的值最小?最小值是多少?
的值最小?最小值是多少?
(3)根据(2)中的结论,请构造图形求代数式![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 城有肥料200吨,
城有肥料200吨,![]() 城有肥料300吨.现将这些肥料全部运往
城有肥料300吨.现将这些肥料全部运往![]() ,
,![]() 两乡.
两乡. ![]() 乡需要的肥料比
乡需要的肥料比![]() 乡少20吨.从
乡少20吨.从![]() 城运往
城运往![]() ,
,![]() 两乡的费用分别为每吨20元和25元;从
两乡的费用分别为每吨20元和25元;从![]() 城运往
城运往![]() ,
,![]() 两乡的费用分别为每吨15元和24元.
两乡的费用分别为每吨15元和24元.
(1)求![]() ,
,![]() 两乡各需肥料多少吨?
两乡各需肥料多少吨?
(2)设从![]() 城运往
城运往![]() 乡的肥料为
乡的肥料为![]() 吨,全部肥料运往
吨,全部肥料运往![]() ,
,![]() 两乡的总运费为
两乡的总运费为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)因近期持续暴雨天气,为安全起见,从![]() 城到
城到![]() 乡需要绕道运输,实际运费每吨增加了
乡需要绕道运输,实际运费每吨增加了![]() 元(
元(![]() ),其它路线运费不变.此时全部肥料运往
),其它路线运费不变.此时全部肥料运往![]() ,
,![]() 两乡所需最少费用为10520元,则
两乡所需最少费用为10520元,则![]() 的值为__ (直接写出结果).
的值为__ (直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com