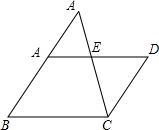
(1)证明:四边形ABCD是平行四边形,
∴AB=DC,AB∥DC.
∴∠FAE=AD,∠F=∠ECD.
又∵EA=ED,
∴△AFE≌△DCE,
∴AF=DC,
AF=AB.
(2)∵A(1,0)、B(5,0),
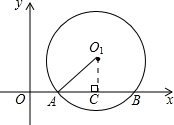
∴AB=4,
过点O
1作O
1C⊥x轴于C,
∴AC=BC=

AB=2,∠O
1CA=90°,
∵点O
1的纵坐标为

,
∴O
1C=

,
∴AO
1=3.
∴⊙O
1的半径为3.
分析:(1)根据平行四边形的性质,可得AB∥CD,AB=CD,所以∠F=∠FCD,又由AE=DE,∠AEF=∠DEC,证得△AFE≌△DCE,问题得证;
(2)此题可以利用垂径定理求解.注意应用勾股定理求解.
点评:(1)考查了平行四边形的性质:平行四边形的对边平行且相等.还考查了全等三角形的判定与性质;
(2)此题考查了垂径定理:垂直于弦的直径平分弦及平分弦所对的两条弧,注意勾股定理的应用.

 ,求⊙O1的半径.
,求⊙O1的半径.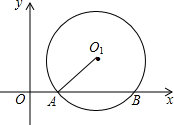

 AB=2,∠O1CA=90°,
AB=2,∠O1CA=90°, ,
, ,
,

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案