
【题目】如图(1),抛物线![]() 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,![]() ).[图(2)为解答备用图]
).[图(2)为解答备用图]
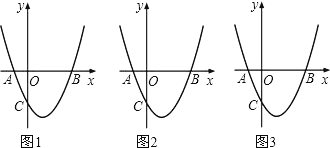
(1)![]() __________,点A的坐标为___________,点B的坐标为__________;
__________,点A的坐标为___________,点B的坐标为__________;
(2)设抛物线![]() 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
【答案】(1) k=-3,A(-1,0),B(3,0);(2)9;(3) ![]() .
.
【解析】
试题分析:(1)将C点坐标代入抛物线的解析式中,即可求出k的值;令抛物线的解析式中y=0,即可求出A、B的坐标;
(2)将抛物线的解析式化为顶点式,即可求出M点的坐标;由于四边形ACMB不规则,可连接OM,将四边形ACMB的面积转化为△ACO、△MOC以及△MOB的面积和;
(3)当D点位于第三象限时四边形ABCD的最大面积显然要小于当D位于第四象限时四边形ABDC的最大面积,因此本题直接考虑点D为与第四象限时的情况即可;设出点D的横坐标,根据抛物线的解析式即可得到其纵坐标;可参照(2)题的方法求解,连接OD,分别表示出△ACO、△DOC以及△DOB的面积,它们的面积和即为四边形ABDC的面积,由此可得到关于四边形ABDC的面积与D点横坐标的函数关系式,根据函数的性质即可求出四边形ABDC的最大面积及对应的D点坐标.
试题解析:(1)由于点C在抛物线的图象上,则有:k=-3;
∴y=x2-2x-3;
令y=0,则x2-2x-3=0,
解得x=-1,x=3,
∴A(-1,0),B(3,0);
(2)抛物线的顶点为M(1,-4),连接OM;
则△AOC的面积=![]() AOOC=
AOOC=![]() ×1×3=
×1×3=![]() ,
,
△MOC的面积=![]() OC|xM|=
OC|xM|=![]() ×3×1=
×3×1=![]() ,
,
△MOB的面积=![]() OB|yM|=
OB|yM|=![]() ×3×4=6;
×3×4=6;
∴四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=9;
(3)设D(m,m2-2m-3),连接OD;
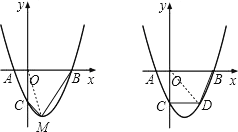
则0<m<3,m2-2m-3<0;
且△AOC的面积=![]() ,△DOC的面积=
,△DOC的面积=![]() m,△DOB的面积=-
m,△DOB的面积=-![]() (m2-2m-3);
(m2-2m-3);
∴四边形ABDC的面积=△AOC的面积+△DOC的面积+△DOB的面积
=-![]() m2+
m2+![]() m+6=-
m+6=-![]() (m-
(m-![]() )2+
)2+![]() ;
;
∴存在点D(![]() ,-
,-![]() ),使四边形ABDC的面积最大,且最大值为
),使四边形ABDC的面积最大,且最大值为![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
(1)本次被调查的学员共有 人;在被调查者中参加“科目3”测试的有 人;将条形统计图补充完整;
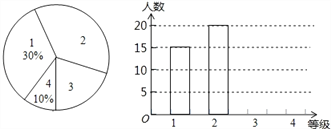
(2)该考点参加“科目4”考试的学员里有3位是教师,某新闻部门准备在该考点参加“科目4”考试的学员中随机选出2位,调查他们对新规的了解情况,请你用列表法或画树状图的方法求出所选两位学员恰好都是教师的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 将最后一名老师送到目的地时,小王距出发地多少千米?方位如何?
将最后一名老师送到目的地时,小王距出发地多少千米?方位如何?
![]() 若汽车耗油量为
若汽车耗油量为![]() 升/千米,则当天耗油多少升?若汽油价格为
升/千米,则当天耗油多少升?若汽油价格为![]() 元/升,则小王共花费了多少元钱?
元/升,则小王共花费了多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:如图,在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点
的图象交于点![]() 和点和
和点和![]() .
.
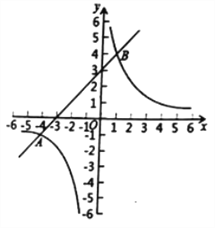
(1)求这两个函数的表达式;
(2)观察图象,当![]() 时,直接写出自变量
时,直接写出自变量![]() 的取值范围;
的取值范围;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线y![]() x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是_____.
x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
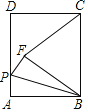
【题目】如图,在矩形ABCD中,AB=5,BC=6,P为AD上一动点,把△ABP沿BP翻折,使点A落在点F处,连接CF,若BF=CF,则AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材的![]() 课题学习
课题学习![]() 要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
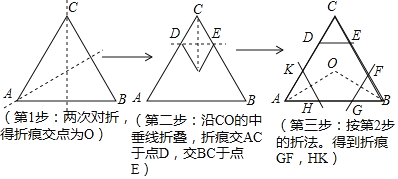
请你根据小明同学的折叠方法,回答以下问题: ![]() 如果设正三角形ABC的边长为a,那么
如果设正三角形ABC的边长为a,那么![]() ______
______ ![]() 用含a的式子表示
用含a的式子表示![]() ;
;
![]() 根据折叠性质可以知道
根据折叠性质可以知道![]() 的形状为______ 三角形;
的形状为______ 三角形;
![]() 请同学们利用
请同学们利用![]() 、
、![]() 的结论,证明六边形KHGFED是一个六边形.
的结论,证明六边形KHGFED是一个六边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭![]() 出发,晚上停留在
出发,晚上停留在![]() 处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
+5,-8,+10,-12,+6,-18,+5,-2.
(1)![]() 处在岗亭
处在岗亭![]() 的什么方向?距离岗亭
的什么方向?距离岗亭![]() 多远?
多远?
(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com