
����Ŀ����2020�ȷ���������������������3��22����ǹ���ܣ����α�����������Ŀ��A��ȫ�������ɣ�B����������ɣ�C�����������ɣ�С����С�춼������������µ�־Ը�߷������������˶��ѱ�ѡ�У���ʱ��ί����������Ƿ��䵽������Ŀ�飮
��1��С�������䵽�����������ɡ���Ŀ��ĸ���Ϊ�� ����
��2����������״ͼ���б��������˱����䵽ͬһ����Ŀ��ĸ��ʣ�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У���
����![]() ���
��б��![]() �ϣ���
�ϣ���![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ���ֱ���
Ϊ�뾶��Բ���ֱ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ������
������![]() ����֪
����֪![]() .
.
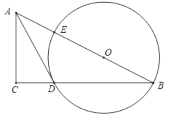
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() �����ӻ�
�����ӻ�![]() ����
����![]() ��Χ��Ӱͼ�ε������
��Χ��Ӱͼ�ε������
��3����![]() ��
��![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
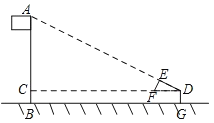
����Ŀ����ͼ��ijУ��ѧ��ȤС���������Ƶ�ֱ��������Ӳֽ��DEF�������ٳ����AB�ĸ߶ȣ�����ͨ����������λ�ã�ʹб��DF����汣��ƽ�У���ʹ��DE����˶���A��ͬһֱ���ϣ���֪DE=0.5m��EF=0.25m��Ŀ���D������ľ���DG=1.5m������˵�ˮƽ����DC=20m������˵ĸ߶�Ϊ( )
A.![]() mB.
mB.![]() m
m
C.11.5mD.10m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
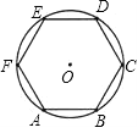
����Ŀ����ͼ����֪![]() ���ܳ�����
���ܳ�����![]() ���������ڽ���������ABCDEF������ǣ� ��
���������ڽ���������ABCDEF������ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2��![]() x+c��x���ཻ�ڵ�A����2��0����B��4��0������y���ཻ�ڵ�C������AC��BC�����߶�BCΪֱ������M������C��ֱ��CE��AB���������ߺ͡�M�ֱ��ڵ�D��E����P��BC�·������������˶���
x+c��x���ཻ�ڵ�A����2��0����B��4��0������y���ཻ�ڵ�C������AC��BC�����߶�BCΪֱ������M������C��ֱ��CE��AB���������ߺ͡�M�ֱ��ڵ�D��E����P��BC�·������������˶���
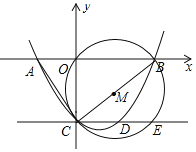
��1����������ߵĽ���ʽ��
��2������PDE����DEΪ�ױߵĵ���������ʱ�����P�����ꣻ
��3�����ı���ACPB��������ʱ�����P�����겢������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
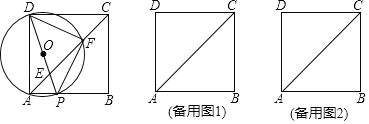
����Ŀ����ͼ����������ABCD�У�AB��4������P�ӵ�A��������ÿ��2����λ���ٶȣ����߶�AB���������˶��������Bֹͣ������DP��AC�ڵ�E����DPΪֱ������O��AC�ڵ�F������DF��PF��
��1����֤����DPFΪ����ֱ�������Σ�
��2������P���˶�ʱ��t�룮
����tΪ��ֵʱ����Eǡ��ΪAC��һ�����ȷֵ㣻
������EFP��PF���ۣ��õ���QFP������Qǡ������BC��ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
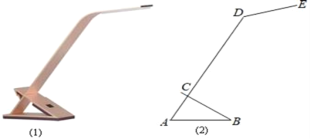
����Ŀ����ͼ��1����һ�ּ���̨�ƣ�����ṹͼ��2���е���Ϊ��ABC��BC������ֲ��ƣ���A��C��D��ͬһֱ���ϣ����á�ACB=90������A=60����AB=16cm����ADE=135�����Ƹ�CD��Ϊ40cm���ƹ�DE��Ϊ15cm�����ο����ݣ�sin15��=0.26��cos15��=0.97��tan15��=0.27��sin30��=0.5��cos30��=0.87��tan30��=0.58����
��1����DE��ˮƽ���棨AB����ֱ�ߣ����ɵĽǣ�
��2����̨�Ƶĸߣ���E������ľ��룬�����ȷ��0.1cm����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Rt��ABC�У�AB��BC����O��AC���е㣬����OB����C����CD��OB����BO���ӳ����ڴ���D��BC��8��sin����![]() ��
��![]()
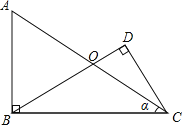
��1���߶�OC�ij���
��2��cos��DOC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
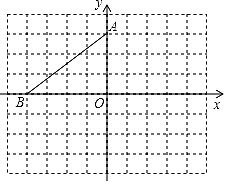
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,��A��B������ֱ���(0,3)��(-4,0)��
(1)����AOB�Ƶ�A��ʱ����ת90��õ���AEF,��O��B��Ӧ��ֱ���E��F,����ͼ�������AEF��
(2)�Ե�OΪλ�����ģ���������AEF��λ�Ʊ任����СΪԭ����![]() �������ڻ���һ������������
�������ڻ���һ������������![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com