
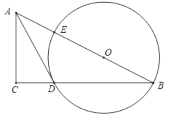
【题目】如图,在![]() 中,点
中,点![]() 在斜边
在斜边![]() 上,以
上,以![]() 为圆心,
为圆心,![]() 为半径作圆,分别与
为半径作圆,分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求劣弧
,求劣弧![]() 与弦
与弦![]() 所围阴影图形的面积;
所围阴影图形的面积;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接![]() ,利用圆的半径相等及已知条件证明
,利用圆的半径相等及已知条件证明![]() ,再根据直角三角形两锐角互余得到
,再根据直角三角形两锐角互余得到![]() ,再根据平角定义即可得到结论;
,再根据平角定义即可得到结论;
(2)连接![]() ,作
,作![]() 于
于![]() ,根据
,根据![]() 及直角三角形的性质求出BD=2,根据垂径定理及三角函数求出,OF,再根据30
及直角三角形的性质求出BD=2,根据垂径定理及三角函数求出,OF,再根据30![]() 角所对的直角边等于斜边的一半求出OB,即可利用扇形面积减去三角形的面积求出阴影部分的面积;
角所对的直角边等于斜边的一半求出OB,即可利用扇形面积减去三角形的面积求出阴影部分的面积;
(3)先证明![]() 求出AB,再根据勾股定理求出半径,即可求得AE的长.
求出AB,再根据勾股定理求出半径,即可求得AE的长.
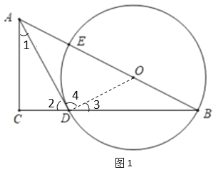
(1)证明:连接![]() ,如图1所示:
,如图1所示:
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
则![]() 为
为![]() 的切线;
的切线;
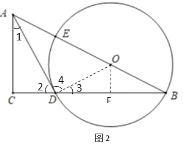
(2)连接![]() ,作
,作![]() 于
于![]() ,如图2所示:
,如图2所示:
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,
∴劣弧![]() 与弦
与弦![]() 所围阴影部分的面积
所围阴影部分的面积
![]() 扇形
扇形![]() 的面积
的面积![]() 的面积
的面积 ;
;
(3)∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,或
,或![]() (舍去),
(舍去),
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴在![]() 中,
中, ![]() ,
,
∴设![]() 的半径为
的半径为![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
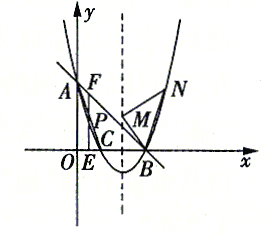
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() 直线
直线![]() 经过点
经过点![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方的抛物线上一动点,过点
下方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() 设点
设点![]() 的横坐标为
的横坐标为![]() 若
若![]() 求
求![]() 的值;
的值;
(3)![]() 是第一象限对称轴右侧抛物线上的一点,连接
是第一象限对称轴右侧抛物线上的一点,连接![]() 抛物线的对称轴上是否存在点
抛物线的对称轴上是否存在点![]() .使得
.使得![]() 与
与![]() 相似,且
相似,且![]() 为直角,若存在,请直接写出点
为直角,若存在,请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() .
.
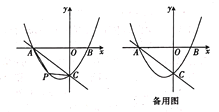
(1)求抛物线的解析式.
(2)点![]() 是抛物线上一动点,设点
是抛物线上一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①若点![]() 在直线
在直线![]() 的下方,当
的下方,当![]() 的面积最大时,求
的面积最大时,求![]() 的值;
的值;
②若![]() 是以
是以![]() 为底的等腰三角形,请直接写出
为底的等腰三角形,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
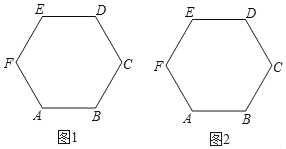
【题目】正六边形ABCDEF的边长1,请仅用无刻度的直尺按要求画图.
(1)在图1中,画出一条长度为![]() 的线段;
的线段;
(2)在图2中,画出一条长度为![]() 的线段,并说明理由.
的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.对角线相等的四边形一定是矩形
B.任意掷一枚质地均匀的硬币10次,一定有5次正面向上
C.如果有一组数据为5,3,6,4,2,那么它的中位数是6
D.“用长分别为![]() 、12cm、
、12cm、![]() 的三条线段可以围成三角形”这一事件是不可能事件
的三条线段可以围成三角形”这一事件是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月,以“寻根国学,传承文明”为主题的兰州市第三届“国学少年强一国学知识挑战赛”总决赛拉开帷幕,小明晋级了总决赛.比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.
第一环节:写字注音、成语故事、国学常识、成语接龙(分别用![]() 表示);
表示);
第二环节:成语听写、诗词对句、经典通读(分别用![]() 表示)
表示)
(1)请用树状图或列表的方法表示小明参加总决赛抽取题目的所有可能结果
(2)求小明参加总决赛抽取题目都是成语题目(成语故事、成语接龙、成语听写)的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个工程队共同参与一项筑路工程,甲队单独施工3个月,这时增加了乙队,两队又共同工作了2个月,总工程全部完成,已知甲队单独完成全部工程比乙队单独完成全部工程多用2个月,设甲队单独完成全部工程需![]() 个月,则根据题意可列方程中错误的是( )
个月,则根据题意可列方程中错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com