
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() 直线
直线![]() 经过点
经过点![]() .
.
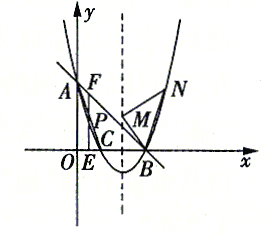
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方的抛物线上一动点,过点
下方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() 设点
设点![]() 的横坐标为
的横坐标为![]() 若
若![]() 求
求![]() 的值;
的值;
(3)![]() 是第一象限对称轴右侧抛物线上的一点,连接
是第一象限对称轴右侧抛物线上的一点,连接![]() 抛物线的对称轴上是否存在点
抛物线的对称轴上是否存在点![]() .使得
.使得![]() 与
与![]() 相似,且
相似,且![]() 为直角,若存在,请直接写出点
为直角,若存在,请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2) ![]() 或
或![]() ;(3)存在,点
;(3)存在,点![]() 坐标为
坐标为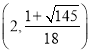 或
或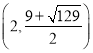
【解析】
(1)先求出点A、B坐标,用待定系数法即求出抛物线解析式;
(2)根据抛物线解析式与直线解析式表示出点P、F的坐标,然后表示出PE、PF,再列出绝对值方程,然后求解即可;
(3)先求出点C的坐标,也就求出OC的长,再设对称轴与![]() 轴交于点
轴交于点![]() 过
过![]() 点作
点作![]() 交对称轴于点
交对称轴于点![]() .根据相似三角形的性质得到KM和MQ的长,进而表示出点N的坐标,最后将点N的坐标代入函数解析式求解即可.
.根据相似三角形的性质得到KM和MQ的长,进而表示出点N的坐标,最后将点N的坐标代入函数解析式求解即可.
![]() 经过点
经过点![]() 分别在
分别在![]() 轴与
轴与![]() 轴上,
轴上,
![]() .
.
![]() 抛物线
抛物线![]() 经过点
经过点![]() ,
,
![]() ,解得
,解得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
![]() 点
点![]() 的横坐标为
的横坐标为![]()
![]() 由题意可知,点
由题意可知,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 当点
当点![]() 在
在![]() 轴上方时,
轴上方时,
![]()
解得![]() 或
或![]() (与点
(与点![]() 重合,舍去).
重合,舍去).
![]()
![]() 当点
当点![]() 在
在![]() 轴下方时,
轴下方时,
![]()
解得![]() 或
或![]() (与点
(与点![]() 重合,舍去).
重合,舍去).
![]()
综上所述,![]() 的值为
的值为![]() 或
或![]()
![]() 存在,点
存在,点![]() 坐标为
坐标为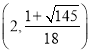 或
或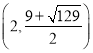
如图,设对称轴与![]() 轴交于点
轴交于点![]() 过
过![]() 点作
点作![]() 交对称轴于点
交对称轴于点![]() .
.
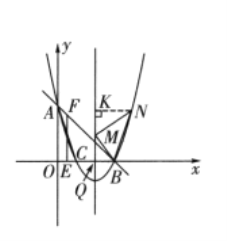
![]() 与
与![]() 轴交于
轴交于![]() 两点,
两点,
![]()
![]()
![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]()
![]() 当
当![]() 时,
时,![]()
由一线三垂直模型得出,
![]() .
.
![]()
![]() 设
设![]()
则![]()
![]()
![]()
![]() 点
点![]() 在抛物线上,
在抛物线上,
![]()
解得![]() (舍).
(舍).
![]() 点
点![]() 的坐标为
的坐标为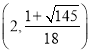
![]() 当
当![]() 时,
时,![]()
同理![]()
![]()
![]() ,
,
设![]()
则![]()
![]()
![]() 即
即![]()
![]() 点
点![]() 在抛物线上,
在抛物线上,
![]()
解得![]() (舍),
(舍),
![]() 点
点![]() 的坐标为
的坐标为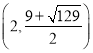
综上所述,存在点![]() 点
点![]() 的坐标为
的坐标为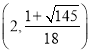 ,
,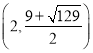


科目:初中数学 来源: 题型:
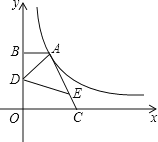
【题目】如图,点A在双曲线y=![]() 的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为
的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为![]() ,则k的值为______.
,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
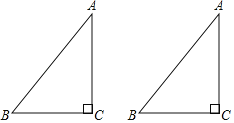
【题目】下面是小宇设计的“作已知直角三角形的中位线”的尺规作图过程.
已知:在△ABC中,∠C=90°.
求作:△ABC的中位线DE,使点D在AB上,点E在AC上.
作法:如图,
①分别以A,C为圆心,大于![]() AC长为半径画弧,两弧交于P,Q两点;
AC长为半径画弧,两弧交于P,Q两点;
②作直线PQ,与AB交于点D,与AC交于点E.
所以线段DE就是所求作的中位线.
根据小宇设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接PA,PC,QA,QC,DC,
∵PA=PC,QA= ,
∴PQ是AC的垂直平分线( )(填推理的依据).
∴E为AC中点,AD=DC.
∴∠DAC=∠DCA,
又在Rt△ABC中,有∠BAC+∠ABC=90°,∠DCA+∠DCB=90°.
∴∠ABC=∠DCB( )(填推理的依据).
∴DB=DC.
∴AD=BD=DC.
∴D为AB中点.
∴DE是△ABC的中位线.
查看答案和解析>>
科目:初中数学 来源: 题型:
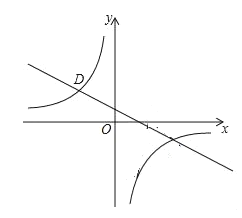
【题目】如图,已知点A(1,a)是反比例函数y1=![]() 的图象上一点,直线y2=﹣
的图象上一点,直线y2=﹣![]() 与反比例函数y1=
与反比例函数y1=![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A |
|
|
B |
|
|
C |
|
|
D |
|
|
E |
|
|
调查结果扇形统计图
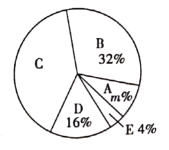
请根据以上图表,解答下列问题:
(1)这次被调查的同学共有______人,![]() ______,
______,![]() _______;
_______;
(2求扇形统计图中C所在的扇形的圆心角度数;.
(3)该校共有学生![]() 人,请估计每月零花钱的数额
人,请估计每月零花钱的数额![]() 在
在![]() 范围内的人数.
范围内的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市地铁1号线全长约60km,市政府通过招标,甲、乙两家地铁工程公司承担了施工任务,根据招标合同可知,甲公司每月计划施工效率是乙公司的1.2倍,则乙公司单独施工比甲公司单独施工多用10个月,且市政府需要支付给甲公司的施工费用为6亿元/km,乙公司的施工费用为5亿元/km.
(1)甲、乙两家地铁工程公司每月计划施工各为多少km?
(2)由于设备和施工现场只能供一家地铁工程公司单独施工的原因,现计划甲、乙两家公司共用55个月恰好完成施工任务(每家公司施工时间不足一个月按照一个整月计算),且甲公司施工时间不得少于乙公司的两倍,应如何安排才能使市政府支付给两家地铁工程公司的总费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,C、E是⊙O上的两点,CE=CB,∠BCD=∠CAE,延长AE交BC的延长线于点F.
(1)求证:CD是⊙O的切线;
(2)求证:CE=CF;
(3)若BD=1,CD=![]() ,求弦AC的长.
,求弦AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 在斜边
在斜边![]() 上,以
上,以![]() 为圆心,
为圆心,![]() 为半径作圆,分别与
为半径作圆,分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
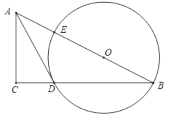
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求劣弧
,求劣弧![]() 与弦
与弦![]() 所围阴影图形的面积;
所围阴影图形的面积;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com