
����Ŀ��ij�е���1����ȫ��Լ60km��������ͨ���б꣬�ס������ҵ������̹�˾�е���ʩ���������б��ͬ��֪����˾ÿ�¼ƻ�ʩ��Ч�����ҹ�˾��1.2�������ҹ�˾����ʩ���ȼ�˾����ʩ������10���£�����������Ҫ֧������˾��ʩ������Ϊ6��Ԫ/km���ҹ�˾��ʩ������Ϊ5��Ԫ/km��
��1���ס������ҵ������̹�˾ÿ�¼ƻ�ʩ����Ϊ����km��
��2�������豸��ʩ���ֳ�ֻ�ܹ�һ�ҵ������̹�˾����ʩ����ԭ���ּƻ��ס������ҹ�˾����55����ǡ�����ʩ������ÿ�ҹ�˾ʩ��ʱ�䲻��һ���°���һ�����¼��㣩���Ҽ�˾ʩ��ʱ�䲻�������ҹ�˾��������Ӧ��ΰ��Ų���ʹ������֧�������ҵ������̹�˾���ܷ������٣�
���𰸡���1����˾ÿ�¼ƻ�ʩ��1.2km���ҹ�˾ÿ��ʩ��1km����2����˾ʩ��37���£��ҹ�˾ʩ��18���£��ܷ������٣�
��������
��1�����ҹ�˾ÿ�¼ƻ�ʩ��x km�����˾ÿ��ʩ��1.2x km�������ҹ�˾����ʩ���ȼ�˾����ʩ������10���£��з�����⣻
��2�����˾ʩ����m���£����ҹ�˾ʩ����55-m�����£���֧�����ܷ���Ϊw��Ԫ�����������г�w��m�ĺ�����ϵʽ�����ݼ�˾ʩ��ʱ�䲻�������ҹ�˾������ȷ��m��ȡֵ��Χ��Ȼ������һ�κ�������������ֵ��
�⣺���ҹ�˾ÿ�¼ƻ�ʩ��x km�����˾ÿ��ʩ��1.2x km��
�������⣬��
![]()
��ã�x=1
�����飬x=1��ԭ���̵ĸ���
��1.2x=1.2��1=1.2
��ˣ���˾ÿ�¼ƻ�ʩ��1.2km���ҹ�˾ÿ��ʩ��1km��
��2�����˾ʩ����m���£����ҹ�˾ʩ����55-m�����£���֧�����ܷ���Ϊw��Ԫ����
w=1.2��6��m+1��5����55-m��=7.2m+275-5m=2.2m+275
��k=2.2��0��w����m�����������
��˾ʩ��ʱ�䲻�������ҹ�˾��������
��![]() ��
��
��![]() ��
��
�൱m=37ʱ��w�����ֵ��
55-37=18��
��ˣ���˾ʩ��37���£��ҹ�˾ʩ��18���£��ܷ������٣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
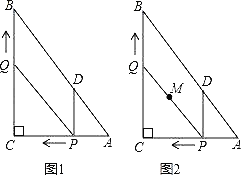
����Ŀ����ͼ1����Rt��ABC�У���C=90�㣬AC=6��BC=8������P�ӵ�A��ʼ�ر�AC���C��1����λ���ȵ��ٶ��˶�������Q�ӵ�C��ʼ�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�������P��PD��BC����AB�ڵ�D������PQ�ֱ�ӵ�A��Cͬʱ������������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1��ֱ���ú�t�Ĵ���ʽ�ֱ��ʾ��QB=�� ����PD=�� ����
��2���Ƿ����t��ֵ��ʹ�ı���PDBQΪ���Σ������ڣ����t��ֵ���������ڣ�˵�����ɣ���̽����θı�Q���ٶȣ������˶�����ʹ�ı���PDBQ��ijһʱ��Ϊ���Σ����Q���ٶȣ�
��3����ͼ2���������˶������У�����߶�PQ�е�M��������·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
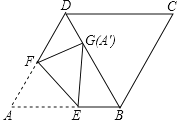
����Ŀ����ͼ��������ABCD�У���ABC=120�㣬�������۵���ʹ��Aǡ�����ڶԽ���BD�ϵĵ�G��������B��D�غϣ����ۺ�ΪEF����DG=2��BG=6����BE�ij�Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ��õ�
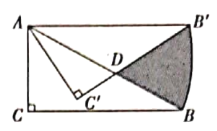
��õ�![]() ����ͼ����Ӱ���ֵ������______��
����ͼ����Ӱ���ֵ������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() ����
����![]() ���㣬��
���㣬��![]() ���ڵ�
���ڵ�![]() ֱ��
ֱ��![]() ������
������![]() ��
��
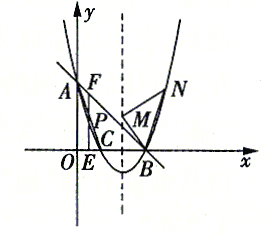
��1���������ߵĽ���ʽ��
��2����![]() ��ֱ��
��ֱ��![]() �·�����������һ���㣬����
�·�����������һ���㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ���
���![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��3��![]() �ǵ�һ���Գ����Ҳ��������ϵ�һ�㣬����
�ǵ�һ���Գ����Ҳ��������ϵ�һ�㣬����![]() �����ߵĶԳ������Ƿ���ڵ�
�����ߵĶԳ������Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ��
��![]() ���ƣ���
���ƣ���![]() Ϊֱ�ǣ������ڣ���ֱ��д����
Ϊֱ�ǣ������ڣ���ֱ��д����![]() �����꣬�������ڣ���˵�����ɣ�
�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��x2��3x+c��y��Ľ���Ϊ��0��2����������˵����ȷ���ǣ�������
A. �����߿�������
B. ��������x��Ľ���Ϊ����1��0������3��0��
C. ��x��1ʱ��y�����ֵΪ0
D. �����ߵĶԳ�����ֱ��x��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
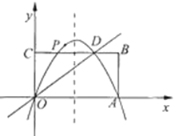
����Ŀ������OABC��ֱ������ϵ�е�λ����ͼ��ʾ��A��C���������ֱ�ΪA(6��0)��C(0��3)��ֱ��y=![]() x��BC���ཻ��D��
x��BC���ཻ��D��
��1�����D�����꣺
��2����������y=ax![]() ��bx����D��A���㣬��ȷ���������ߵı���ʽ��
��bx����D��A���㣬��ȷ���������ߵı���ʽ��
��3��PΪx���Ϸ���2�����е���������һ�㣬���POA��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
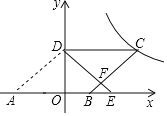
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬ABCD�ı�AB��x���ϣ�����D��y����������ϣ���C�ڵ�һ���ޣ�����AOD��y�ᷭ�ۣ�ʹ��A����x���ϵĵ�E������Bǡ��ΪOE���е㣬DE��BC���ڵ�F����y![]() ��k��0��ͼ����C����S��BEF��1����k��ֵΪ________��
��k��0��ͼ����C����S��BEF��1����k��ֵΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ��������O����AD�Ĵ��߽���ԲO�ڵ�E����AC�ڵ�C��ʹ��BED=��C��
��1���ж�ֱ��AC��ԲO��λ�ù�ϵ����֤����Ľ��ۣ�
��2����AC=8��cos��BED=![]() ����AD�ij���
����AD�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com