
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到
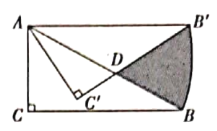
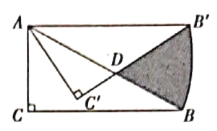
后得到![]() ,则图中阴影部分的面积是______.
,则图中阴影部分的面积是______.
【答案】![]()
【解析】
根据含30度的直角三角形三边的关系得到AB=2AC=4,![]() ,根据互余得到∠CAB=60°,再根据旋转的性质得到AC′=AC=2,AB′=AB=4,B′C′=BC=2
,根据互余得到∠CAB=60°,再根据旋转的性质得到AC′=AC=2,AB′=AB=4,B′C′=BC=2![]() ,∠B′AB=30°,∠C′AB′=∠CAB=60°,则∠C′AD=∠C′AB′∠BAB′=30°,接着在Rt△AC′D中,利用∠C′AD=30°可得C′D=
,∠B′AB=30°,∠C′AB′=∠CAB=60°,则∠C′AD=∠C′AB′∠BAB′=30°,接着在Rt△AC′D中,利用∠C′AD=30°可得C′D=![]() AC′=
AC′=![]() ,所以B′D=B′C′C′D=
,所以B′D=B′C′C′D=![]() ,然后根据三角形面积公式、扇形面积公式和图中阴影部分的面积=S扇形BAB′S△ADB′进行计算即可.
,然后根据三角形面积公式、扇形面积公式和图中阴影部分的面积=S扇形BAB′S△ADB′进行计算即可.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∵将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴题图中阴影部分的面积=![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系![]() 中有点
中有点![]() 和某一函数图象
和某一函数图象![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交图象
轴的垂线,交图象![]() 于点
于点![]() ,设点
,设点![]() ,
,![]() 的纵坐标分别为
的纵坐标分别为![]() ,
,![]() .如果
.如果![]() ,那么称点
,那么称点![]() 为图象
为图象![]() 的上位点;如果
的上位点;如果![]() ,那么称点
,那么称点![]() 为图象
为图象![]() 的图上点;如果
的图上点;如果![]() ,那么称点
,那么称点![]() 为图象
为图象![]() 的下位点.
的下位点.
(1)已知抛物线![]() .
.
① 在点A(-1,0),B(0,-2),C(2,3)中,是抛物线的上位点的是 ;
② 如果点![]() 是直线
是直线![]() 的图上点,且为抛物线的上位点,求点
的图上点,且为抛物线的上位点,求点![]() 的横坐标
的横坐标![]() 的取值范围;
的取值范围;
(2)将直线![]() 在直线
在直线![]() 下方的部分沿直线
下方的部分沿直线![]() 翻折,直线
翻折,直线![]() 的其余部分保持不变,得到一个新的图象,记作图象
的其余部分保持不变,得到一个新的图象,记作图象![]() .⊙
.⊙![]() 的圆心
的圆心![]() 在
在![]() 轴上,半径为
轴上,半径为![]() .如果在图象
.如果在图象![]() 和⊙
和⊙![]() 上分别存在点
上分别存在点![]() 和点F,使得线段EF上同时存在图象
和点F,使得线段EF上同时存在图象![]() 的上位点,图上点和下位点,求圆心
的上位点,图上点和下位点,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上,以
上,以![]() 为直径的
为直径的![]() 与
与![]() 相交于点
相交于点![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() .
.
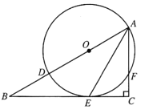
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)在(1)的条件下,判断以![]() 为顶点的四边形为哪种特殊四边形,并说明理由.
为顶点的四边形为哪种特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
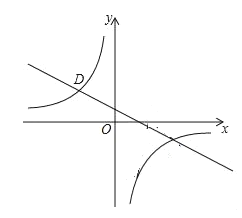
【题目】如图,已知点A(1,a)是反比例函数y1=![]() 的图象上一点,直线y2=﹣
的图象上一点,直线y2=﹣![]() 与反比例函数y1=
与反比例函数y1=![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.

(1)求一次函数的解析式;
(2)根据图象直接写出![]() ,时
,时![]() 的取值范围;
的取值范围;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市地铁1号线全长约60km,市政府通过招标,甲、乙两家地铁工程公司承担了施工任务,根据招标合同可知,甲公司每月计划施工效率是乙公司的1.2倍,则乙公司单独施工比甲公司单独施工多用10个月,且市政府需要支付给甲公司的施工费用为6亿元/km,乙公司的施工费用为5亿元/km.
(1)甲、乙两家地铁工程公司每月计划施工各为多少km?
(2)由于设备和施工现场只能供一家地铁工程公司单独施工的原因,现计划甲、乙两家公司共用55个月恰好完成施工任务(每家公司施工时间不足一个月按照一个整月计算),且甲公司施工时间不得少于乙公司的两倍,应如何安排才能使市政府支付给两家地铁工程公司的总费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,以
,以![]() 为弦的
为弦的![]() 与
与![]() 相切于点
相切于点![]() .
.
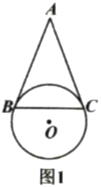
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)将![]() 中
中![]() 以下部分沿直线
以下部分沿直线![]() 向上翻折.
向上翻折.
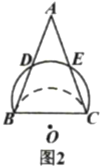
①如图2,若翻折后的弧过![]() 中点
中点![]() ,并交
,并交![]() 于点
于点![]() ,请判断
,请判断![]() 与
与![]() 的关系,并说明理由.
的关系,并说明理由.
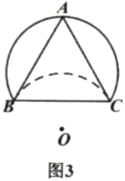
②如图3,若![]() ,且翻折后的弧恰好过点
,且翻折后的弧恰好过点![]() ,则
,则![]() 的半径为________.
的半径为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com