
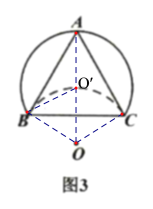
【题目】如图1,在![]() 中,
中,![]() ,以
,以![]() 为弦的
为弦的![]() 与
与![]() 相切于点
相切于点![]() .
.
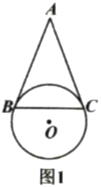
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)将![]() 中
中![]() 以下部分沿直线
以下部分沿直线![]() 向上翻折.
向上翻折.
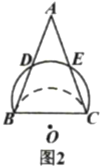
①如图2,若翻折后的弧过![]() 中点
中点![]() ,并交
,并交![]() 于点
于点![]() ,请判断
,请判断![]() 与
与![]() 的关系,并说明理由.
的关系,并说明理由.
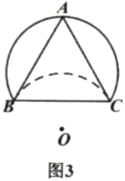
②如图3,若![]() ,且翻折后的弧恰好过点
,且翻折后的弧恰好过点![]() ,则
,则![]() 的半径为________.
的半径为________.
【答案】(1)见解析;(2)①![]() ,见解析,②2
,见解析,②2
【解析】
(1)连接OB,OC,根据等腰三角形的性质,得∠ABC=∠ACB,∠OBC=∠OCB,结合∠ABO=90°,即可得到结论;
(2)①连接DE,BE,由圆周角定理得![]() ,从而得
,从而得![]() ,进而得DE∥BC,由点D是AB的中点,可得DE是ABC的中位线,进而即可得到结论;②连接AO,BO,CO,设AO交
,进而得DE∥BC,由点D是AB的中点,可得DE是ABC的中位线,进而即可得到结论;②连接AO,BO,CO,设AO交![]() 于点O′,易得
于点O′,易得![]() 是
是![]() 所在圆的直径,记
所在圆的直径,记![]() 交弧
交弧![]() 于点
于点![]() ,两圆半径相等,那么点
,两圆半径相等,那么点![]() 就是
就是![]() 所在的圆的圆心,可得O′BO是等边三角形,再利用解直角三角形,即可得到答案.
所在的圆的圆心,可得O′BO是等边三角形,再利用解直角三角形,即可得到答案.
(1)连接OB,OC,
∵AB=AC,OB=OC,
∴∠ABC=∠ACB,∠OBC=∠OCB,
∴∠ABO=∠ACO,
∵AB是![]() 的切线,
的切线,
∴∠ABO=90°,
∴∠ACO=90°,
∴AC是![]() 的切线;
的切线;
(2)①![]() ,理由如下:
,理由如下:
连接DE,BE,
∵AB=AC,
∴∠ABC=∠ACB,
∴![]() ,
,
∴![]() ,即:
,即:![]() ,
,
∴∠BED=∠CBE,
∴DE∥BC,
∴∠ADE=∠ABC=∠ACB=∠AED,
∴AD=AE,
∵点D是AB的中点,
∴AD=![]() AB,
AB,
∴AE=![]() AC,
AC,
∴点E是AC的中点,
∴DE是ABC的中位线,
∴DE=![]() BC.
BC.
综上所述:DE∥BC,DE=![]() BC;
BC;
②连接AO,BO,CO,设AO交![]() 于点O′,
于点O′,
∵翻折后的弧恰好过点![]() ,∠ABO=90°,
,∠ABO=90°,
∴AO是![]() 所在圆的直径,
所在圆的直径,
∵![]() 所在圆与
所在圆与![]() 所在圆是等圆,
所在圆是等圆,
∴OO′既是![]() 所在圆的半径,也是
所在圆的半径,也是![]() 所在圆的半径,
所在圆的半径,
∴点O′是![]() 所在圆的圆心,
所在圆的圆心,
∴O′B=O′O=OB,
∴O′BO是等边三角形,即∠AOB=60°,
∴在RtAOB中,AO=AB÷sin60°=![]() =4,
=4,
∴OO′=2,
即:![]() 的半径为2.
的半径为2.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
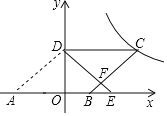
【题目】如图,在平面直角坐标系中,O为坐标原点,ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y![]() (k≠0)图象经过点C,且S△BEF=1,则k的值为________.
(k≠0)图象经过点C,且S△BEF=1,则k的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AC为直径,弧AE=弧BD,BE⊥DC交DC的延长线于点E.
(1)求证:∠1=∠BCE;
(2)求证:BE是⊙O的切线;
(3)若EC=1,CD=3,求cos∠DBA.

查看答案和解析>>
科目:初中数学 来源: 题型:
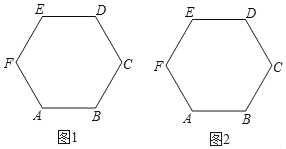
【题目】正六边形ABCDEF的边长1,请仅用无刻度的直尺按要求画图.
(1)在图1中,画出一条长度为![]() 的线段;
的线段;
(2)在图2中,画出一条长度为![]() 的线段,并说明理由.
的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A﹣B﹣C路线对索道进行检修维护.如图:已知![]() 米,
米,![]() 米,AB与水平线
米,AB与水平线![]() 的夹角是
的夹角是![]() ,BC与水平线
,BC与水平线![]() 的夹角是
的夹角是![]() .求:本次检修中,检修人员上升的垂直高度
.求:本次检修中,检修人员上升的垂直高度![]() 是多少米?(结果精确到1米,参考数据:
是多少米?(结果精确到1米,参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() 的图象G经过点
的图象G经过点![]() ,直线
,直线![]() 与y轴交于点B,与图象G交于点C.
与y轴交于点B,与图象G交于点C.
(1)求m的值.
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,C之间的部分与线段BA,BC围成的区域(不含边界)为W.
①当直线l过点![]() 时,直接写出区域W内的整点个数.
时,直接写出区域W内的整点个数.
②若区域W内的整点不少于4个,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中.对角线AC、BD交于点
中.对角线AC、BD交于点![]() .点
.点![]() ,点
,点![]() 分别在线段
分别在线段![]() ,线段
,线段![]() 上,且
上,且![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,
(1)如图1,若点![]() 为线段
为线段![]() 中点,
中点,![]() 求
求![]() 的长;
的长;
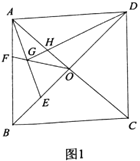
(2)如图2,若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
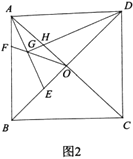
(3)如图3,点![]() 在线段
在线段![]() (含端点)上运动.连接
(含端点)上运动.连接![]() ,当线段
,当线段![]() 长度取得最大值时,直接写出
长度取得最大值时,直接写出![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com