
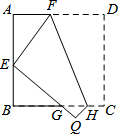
 如图,已知正方形ABCD边长为6,将其折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是( )
如图,已知正方形ABCD边长为6,将其折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是( )| A. | 15 | B. | 12 | C. | 8 | D. | 6 |
分析 根据翻折的性质可得DF=EF,设EF=x,表示出AF,然后利用勾股定理列方程求出x,从而得到AF、EF的长,再求出△AEF和△BGE相似,根据相似三角形对应边成比例列式求出BG、EG,然后根据三角形周长的定义列式计算即可得解.
解答 解:由翻折的性质得,DF=EF,设EF=x,则AF=6-x.
∵点E是AB的中点,
∴AE=BE=$\frac{1}{2}$×6=3.
在Rt△AEF中,AE2+AF2=EF2,即32+(6-x)2=x2.
解得x=$\frac{15}{4}$.
∴AF=6-$\frac{15}{4}$=$\frac{9}{4}$.
∵∠FEG=∠D=90°,
∴∠AEF+∠BEG=90°.
∵∠AEF+∠AFE=90°,
∴∠AFE=∠BEG.
又∵∠A=∠B=90°,
∴△AEF∽△BGE.
∴$\frac{BE}{AF}$=$\frac{BG}{EF}$=$\frac{EG}{EF}$,即$\frac{3}{\frac{9}{4}}$=$\frac{BG}{3}$=$\frac{EG}{\frac{15}{4}}$.
解得:BG=4,EG=5.
∴△EBG的周长=3+4+5=12.
故选:B.
点评 本题考查了翻折变换的性质,勾股定理,相似三角形的判定与性质,熟记性质并求出△AEF的各边的长,然后利用相似三角形的性质求出△EBG的各边的长是解题的关键.


科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:填空题
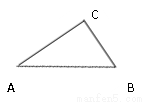
如图,AC⊥BC, 且BC=6,AC=8,AB=10,则点B到AC的距离是 .
A. 6 B. 7 C. 8 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
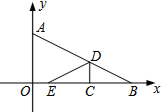 如图,点A(0,2),B(4,0)两点的坐标,将△ABO沿着垂直于x轴的线段CD折叠(点C在x轴上,点D在AB上,点D不与A,B重合),如图,使点E落在x轴上.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.
如图,点A(0,2),B(4,0)两点的坐标,将△ABO沿着垂直于x轴的线段CD折叠(点C在x轴上,点D在AB上,点D不与A,B重合),如图,使点E落在x轴上.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 内含 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | |
| 成本(元/套) | 25 | 28 |
| 售价(元/套) | 30 | 34 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
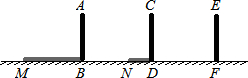
| A. | AB=BC | B. | AB=$\frac{1}{2}$AC | C. | 2AB=AC | D. | AB+BC=AC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com