
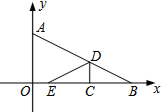
 ��ͼ����A��0��2����B��4��0����������꣬����ABO���Ŵ�ֱ��x����߶�CD�۵�����C��x���ϣ���D��AB�ϣ���D����A��B�غϣ�����ͼ��ʹ��E����x���ϣ����C������Ϊ��x��0������CDE���ABO�ص����ֵ����ΪS��
��ͼ����A��0��2����B��4��0����������꣬����ABO���Ŵ�ֱ��x����߶�CD�۵�����C��x���ϣ���D��AB�ϣ���D����A��B�غϣ�����ͼ��ʹ��E����x���ϣ����C������Ϊ��x��0������CDE���ABO�ص����ֵ����ΪS������ ��1��OB=4��C���λ��Ӧ����������������ۣ���C��OB���е�����е���B֮��ʱ���غϲ����ǡ�CDE����C��OB���е���O֮��ʱ���غϲ��������Σ��Ϳ��Եõ���������ʽ��
��2�����S��x֮��ĺ�������ʽ�����ݺ��������ʾͿ��Եõ��������ֵ��
��3���֡�ADE�Ե�AΪֱ�Ƕ���͡�ADE�Ե�EΪֱ�Ƕ��㣬��������������ۣ��������������εĶ�Ӧ�ߵı���ȣ����OE�ij����Ϳ��Եõ�C������꣮
��� �⣺��1���ٵ�E��ԭ���x����������ʱ���ص������ǡ�CDE��
��S��CDE=$\frac{1}{2}$BC��CD=$\frac{1}{2}$��4-x����-$\frac{1}{2}$x+2��
=$\frac{1}{4}$x2-2x+4��
��E��O�غ�ʱ��CE=$\frac{1}{2}$BO=2����2��x��4��
�ڵ�E��x��ĸ�������ʱ����DE��y�ύ�ڵ�F�����ص�����Ϊ���Σ�
�ߡ�OFE�ס�OAB
��$\frac{OF}{OE}$=$\frac{OA}{OB}$=$\frac{1}{2}$��
��OF=$\frac{1}{2}$OE��
�֡�OE=4-2x��
��OF=$\frac{1}{2}$��4-2x��=2-x��
��S�ı���CDFO=$\frac{x}{2}$��[2-x+��-$\frac{1}{2}$x+2��]��
=-$\frac{3}{4}$x2+2x��
����C���O�غ�ʱ����C������Ϊ��0��0��
��0��x��2��
�ۺϢ٢ڵ�S=$\left\{\begin{array}{l}{\frac{1}{4}{x}^{2}-2x+4��2��x��4��}\\{-\frac{3}{4}{x}^{2}+2x��0��x��2��}\end{array}\right.$��
��2���ٵ�2��x��4ʱ��S=$\frac{1}{4}$x2-2x+4=$\frac{1}{4}$��x-4��2��
��Գ�����ֱ��x=4
�������߿������ϣ�
����2��x��4�У�S��x���������С
�൱x=2ʱ��S���ֵ=$\frac{1}{4}$����2-4��2=1��
�ڵ�0��x��2ʱ��S=-$\frac{3}{4}$x2+2x=-$\frac{3}{4}$��x-$\frac{4}{3}$��2+$\frac{4}{3}$��
��Գ�����ֱ��x=$\frac{4}{3}$��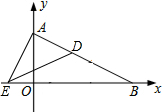
�������߿������£�
�൱x=$\frac{4}{3}$ʱ��S�����ֵΪ$\frac{4}{3}$��
�ۺϢ٢ڵ�x=$\frac{4}{3}$ʱ��S�����ֵΪ$\frac{4}{3}$��
��3�����ڣ���C������Ϊ��$\frac{3}{2}$��0���ͣ�$\frac{5}{2}$��0����
������⣺�ٵ���ADE�Ե�AΪֱ�Ƕ���ʱ����AE��AB��x�Ḻ�����ڵ�E��
�ߡ�AOE�ס�BOA
��$\frac{EO}{AO}$=$\frac{AO}{BO}$=$\frac{1}{2}$��
��AO=2��
��EO=1��
���E������-1��0����
���C��������$\frac{3}{2}$��0����
�ڵ���ADE�Ե�EΪֱ�Ƕ���ʱ��
ͬ���С�AOE�ס�BOA����$\frac{OE}{AO}$=$\frac{OA}{BO}$=$\frac{1}{2}$��
��EO=1��
��E��1��0����
���C�����꣨$\frac{5}{2}$��0����
�ۺϢ٢�֪���������������У�$\frac{3}{2}$��0���ͣ�$\frac{5}{2}$��0����
���� �����ۺϿ����������ۺ��⣮�����漰���˴���ϵ��������κ����Ľ���ʽ�����κ�����ֵ�������������ε��ж��������Լ�������������֪ʶ�㣮�����ѶȽϴ�ע�����պ���˼�롢��������˼�������ν��˼���Ӧ�ã�


 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015-2016ѧ�����ɹŰ��������ٺ������꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
�����μ���һ���������������ش���30���⣬��Ŀ�����ֱ��������ģ����һ���5�֣�һ������1�֣��������ξ����ж����ĵ÷�Ҫ����100�֣���ô������Ҫ���_____��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
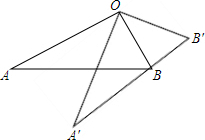 ��ͼ����AOB=90�㣬��Rt��OAB�Ƶ�O����ʱ�뷽����ת��Rt��OA��B�䣬ʹ��Bǡ�����ڱ�A��B���ϣ���֪tanB=2��OB=5����BB��=2$\sqrt{5}$��
��ͼ����AOB=90�㣬��Rt��OAB�Ƶ�O����ʱ�뷽����ת��Rt��OA��B�䣬ʹ��Bǡ�����ڱ�A��B���ϣ���֪tanB=2��OB=5����BB��=2$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
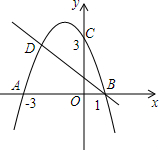 ��ͼ�����κ�����ͼ����x���ཻ��A��-3��0����B��1��0�����㣬��y���ཻ�ڵ�C��0��3������C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ�����ͼ�����B��D��
��ͼ�����κ�����ͼ����x���ཻ��A��-3��0����B��1��0�����㣬��y���ཻ�ڵ�C��0��3������C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ�����ͼ�����B��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
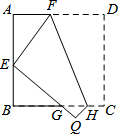 ��ͼ����֪������ABCD�߳�Ϊ6�������۵���ʹ��D����AB�ߵ��е�E�����ۺ�ΪFH����C����Q����EQ��BC���ڵ�G�����EBG���ܳ��ǣ�������
��ͼ����֪������ABCD�߳�Ϊ6�������۵���ʹ��D����AB�ߵ��е�E�����ۺ�ΪFH����C����Q����EQ��BC���ڵ�G�����EBG���ܳ��ǣ�������| A�� | 15 | B�� | 12 | C�� | 8 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com