
分析 (1)移项后得到x2-5x+6=0,再利用因式分解法解方程即可;
(2)利用平方差公式分解因式得到(x+1+2x)(x+1-2x)=0,再解两个一元一次方程即可.
解答 解:(1)∵x2+6=5x,
∴x2-5x+6=0,
∴(x-2)(x-3)=0,
∴x-2=0或x-3=0,
∴x1=2,x2=3;
(2)∵(x+1)2=4x2,
∴(x+1)2-4x2=0,
∴(x+1+2x)(x+1-2x)=0,
∴(3x+1)(x-1)=0,
∴x1=-$\frac{1}{3}$,x2=1.
点评 本题考查了解一元二次方程-因式分解法:把一元二次方程变形为一般式,再把方程左边进行因式分解,然后把方程转化为两个一元一次方程,解这两个一元一次方程得到原方程的解.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
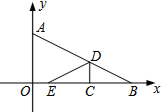 如图,点A(0,2),B(4,0)两点的坐标,将△ABO沿着垂直于x轴的线段CD折叠(点C在x轴上,点D在AB上,点D不与A,B重合),如图,使点E落在x轴上.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.
如图,点A(0,2),B(4,0)两点的坐标,将△ABO沿着垂直于x轴的线段CD折叠(点C在x轴上,点D在AB上,点D不与A,B重合),如图,使点E落在x轴上.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | |
| 成本(元/套) | 25 | 28 |
| 售价(元/套) | 30 | 34 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,以扇形OAB的顶点为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(4,0).若抛物线y=$\frac{1}{4}$x2+k,与扇形OAB的边界总有两个公共点,则实数k的取值范围是-4<k<1.
如图,以扇形OAB的顶点为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(4,0).若抛物线y=$\frac{1}{4}$x2+k,与扇形OAB的边界总有两个公共点,则实数k的取值范围是-4<k<1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
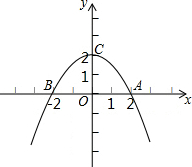 已知如图所示,抛物线y=-$\frac{1}{2}$x2+m-3与x轴交于A,B 两点.且OA=OC.求:
已知如图所示,抛物线y=-$\frac{1}{2}$x2+m-3与x轴交于A,B 两点.且OA=OC.求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=BC | B. | AB=$\frac{1}{2}$AC | C. | 2AB=AC | D. | AB+BC=AC |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com