
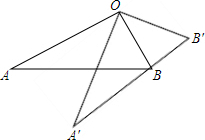
 如图,∠AOB=90°,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanB=2,OB=5,则BB′=2$\sqrt{5}$.
如图,∠AOB=90°,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanB=2,OB=5,则BB′=2$\sqrt{5}$. 分析 根据旋转的性质得出△OAB≌△OA′B′,则有OB=OB′.根据勾股定理,可得B′D的长,根据等腰三角形的性质,可得答案.
解答 解:根据旋转得△OAB≌△OA′B′,
∴OB=OB′,∠ABO=∠B′,
如图,过O作OD⊥BB′,则D为BB′的中点,
∴tanB′=$\frac{OD}{B′D}$=2,
得OD=2B′D.
在Rt△B′OD中,由勾股定理,得
OD2+B′D2=OB′2,
(2B′D)2+B′D2=52.
解得:B′D=$\sqrt{5}$或B°D=-$\sqrt{5}$(不符合题意舍).
由等腰三角形的性质,得BB′=2B′D=2$\sqrt{5}$.
故答案为:2$\sqrt{5}$.
点评 本题考查了旋转的性质,利用了旋转前后的图形全等,利用狗定理得出B′D是解题关键,又利用了全等三角形的性质.


科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:判断题
某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
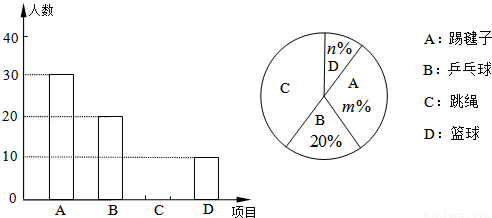
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有 。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
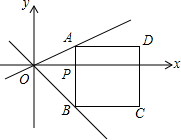 如图,直角坐标系中,点P(t,0)是x轴上的一个动点,过点P作y轴的平行线,分别与直线y=$\frac{1}{2}$x,直线y=-x交于A,B两点,以AB为边向右侧作正方形ABCD.
如图,直角坐标系中,点P(t,0)是x轴上的一个动点,过点P作y轴的平行线,分别与直线y=$\frac{1}{2}$x,直线y=-x交于A,B两点,以AB为边向右侧作正方形ABCD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
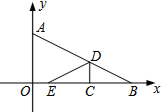 如图,点A(0,2),B(4,0)两点的坐标,将△ABO沿着垂直于x轴的线段CD折叠(点C在x轴上,点D在AB上,点D不与A,B重合),如图,使点E落在x轴上.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.
如图,点A(0,2),B(4,0)两点的坐标,将△ABO沿着垂直于x轴的线段CD折叠(点C在x轴上,点D在AB上,点D不与A,B重合),如图,使点E落在x轴上.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 内含 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com