
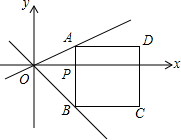
 如图,直角坐标系中,点P(t,0)是x轴上的一个动点,过点P作y轴的平行线,分别与直线y=$\frac{1}{2}$x,直线y=-x交于A,B两点,以AB为边向右侧作正方形ABCD.
如图,直角坐标系中,点P(t,0)是x轴上的一个动点,过点P作y轴的平行线,分别与直线y=$\frac{1}{2}$x,直线y=-x交于A,B两点,以AB为边向右侧作正方形ABCD.分析 (1)根据点P的横坐标利用两条直线的解析式求出PA、PB的长度,再求出正方形的边长AB,然后根据正方形的周长公式列式计算即可得解;
(2)根据点P的横坐标表示出AB,再分①t<0时,点C的横坐标大于2列出不等式求解即可;②t>0时,点P的横坐标小于2点C的横坐标大于2列出不等式求解即可.
解答 解:(1)t=2时,PA=$\frac{1}{2}$×2=1,
PB=|-1×2|=2,
∴AB=PA+PB=1+2=3,
∴正方形ABCD的周长=4AB=4×3=12;
(2)∵点P(t,0),AB∥y轴,
∴点A(t,$\frac{1}{2}$t),B(t,-t),
∴AB=|$\frac{1}{2}$t-(-t)|=|$\frac{3}{2}$t|,
①t<0时,点C的横坐标为t-$\frac{3}{2}$t=-$\frac{1}{2}$t,
∵点(4,0)在正方形ABCD内部,
∴-$\frac{1}{2}$t>4,
解得t<-8,
②t>0时,点C的横坐标为t+$\frac{3}{2}$t=$\frac{5}{2}$t,
∵点(4,0)在正方形ABCD内部,
∴$\frac{5}{2}$t>4,且t<4,
解得t>$\frac{8}{5}$且t<4,
∴$\frac{8}{5}$<t<4,
综上所述,t<-8或 $\frac{8}{5}$<t<4.
故答案为:(1)12;(2)t<-8或 $\frac{8}{5}$<t<4.
点评 本题是一次函数综合题型,主要利用了一次函数图象上点的坐标特征,正方形的性质,难点在于(2)要根据点P的位置分情况讨论.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源:2017届辽宁省大石桥市中考模拟(一)数学试卷(解析版) 题型:单选题
下列事件是必然事件的是( )
A. 任意购买一张电影票,座位号是奇数 B. 打开电视,正在播出“奔跑吧,兄弟”
C. 13名同学中至少有两名同学出生的月份相同 D. 抛掷一枚硬币,反面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.| x | … | … | |||||
| y | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
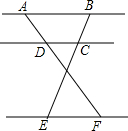 如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )| A. | $\frac{AD}{DF}$=$\frac{BC}{CE}$ | B. | $\frac{BC}{CE}$=$\frac{DF}{AD}$ | C. | $\frac{CD}{EF}$=$\frac{BC}{BE}$ | D. | $\frac{CD}{EF}$=$\frac{AD}{AF}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
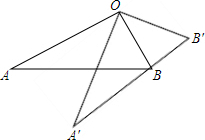 如图,∠AOB=90°,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanB=2,OB=5,则BB′=2$\sqrt{5}$.
如图,∠AOB=90°,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanB=2,OB=5,则BB′=2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com