
�ı���ABCD�������Σ�AC��BD���ཻ�ڵ�O����E��F��ֱ��AD�������㣬��AE=DF��CF����ֱ����Խ���BD����ֱ�߽��ڵ�G������AG��ֱ��AG��BE�ڵ�H��
��1����ͼ1������E��F���߶�AD��ʱ������֤����DAG=��DCG���ڲ���AG��BE��λ�ù�ϵ��������֤����
��2����ͼ2���ڣ�1�������£�����HO����˵��HOƽ�֡�BHG��
��3������E��F�˶�����ͼ3��ʾ��λ��ʱ�������������䣬�뽫ͼ�β�����������ֱ��д����BHO�Ķ�����


�����㡿�ı����ۺ��⣻ȫ�������ε��ж������ʣ������ε����ʣ�
��ר�⡿�ۺ��⣮
����������1���ٸ��������ε����ʵ�DA=DC����ADB=��CDB=45�㣬��ɸ��ݡ�SAS��֤����ADG�ա�CDG�����ԡ�DAG=��DCG���ڸ��������ε����ʵ�AB=DC����BAD=��CDA=90�㣬���ݡ�SAS��֤����ABE�ա�DCF�����ABE=��DCF�����ڡ�DAG=��DCG�����ԡ�DAG=��ABE��Ȼ�����á�DAG+��BAG=90��õ���ABE+��BAG=90�㣬���ǿ��ж�AG��BE��
��2�����ͼ1��ʾ������O��OM��BE�ڵ�M��ON��AG�ڵ�N��֤����AON�ա�BOM���ɵ��ı���OMHNΪ�����Σ����HOƽ�֡�BHG���۳�����
��3�����ͼ2��ʾ���루1��ͬ��������֤��AG��BE������O��OM��BE�ڵ�M��ON��AG�ڵ�N������ȫ�������Ρ�AON�ա�BOM���Ӷ�֤��OMHNΪ�����Σ�����HOƽ�֡�BHG������BHO=45�㣮
����𡿣�1����֤�������ı���ABCDΪ�����Σ�
��DA=DC����ADB=��CDB=45�㣬
�ڡ�ADG�͡�CDG��
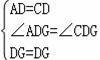
 ��
��
���ADG�ա�CDG��SAS����
���DAG=��DCG��
�ڽ⣺AG��BE���������£�
���ı���ABCDΪ�����Σ�
��AB=DC����BAD=��CDA=90�㣬
�ڡ�ABE�͡�DCF��

 ��
��
���ABE�ա�DCF��SAS����
���ABE=��DCF��
�ߡ�DAG=��DCG��
���DAG=��ABE��
�ߡ�DAG+��BAG=90�㣬
���ABE+��BAG=90�㣬
���AHB=90�㣬
��AG��BE��
��2���⣺�ɣ�1����֪AG��BE��
���ͼ1��ʾ������O��OM��BE�ڵ�M��ON��AG�ڵ�N�����ı���OMHNΪ���Σ�


���MON=90�㣬
�֡�OA��OB��
���AON=��BOM��
�ߡ�AON+��OAN=90�㣬��BOM+��OBM=90�㣬
���OAN=��OBM��
�ڡ�AON���BOM�У�


���AON�ա�BOM��AAS����
��OM=ON��
�����OMHN������
��HOƽ�֡�BHG��
��3����ͼ�β������������ͼ2ʾ����BHO=45�㣮


�루1��ͬ��������֤��AG��BE��
����O��OM��BE�ڵ�M��ON��AG�ڵ�N��
�루2��ͬ��������֤����AON�ա�BOM��
�ɵ�OMHNΪ�����Σ�����HOƽ�֡�BHG��
���BHO=45�㣮
�����������⿼�����ı��ε��ۺ��⣺�������������ε����ʣ���������ȫ�������ε��ж������ʽ���߶κͽ���ȵ����⣮
��


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����˵����ȷ���ǣ�������
�ٴ���ʽ
 ��������a����b������1�ĺͣ�
��������a����b������1�ĺͣ�
��Ҫʹy=
 �����壬��xӦ������0��x��3��
�����壬��xӦ������0��x��3��
�۵�2x��1=0ʱ����ʽ2xy��8x2y+8x3y��ֵ��0��
�ܵ����ϵ�½�����ԼΪ149000000ƽ��ǧ�ף��ÿ�ѧ��������ʾΪ1.49��108ƽ��ǧ�ף�
A���٢� B���٢� C���ڢ� D���ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ�������� �������12��
�������12�� �ǵȱ������Σ���
�ǵȱ������Σ��� ��������
�������� �ڣ��ڶԽ���
�ڣ��ڶԽ��� ����һ��
����һ�� ,ʹ
,ʹ ��С���������СֵΪ�� ��
��С���������СֵΪ�� ��
A�� B��
B�� C��
C�� D��
D��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�ס�������֮��ĸ��ٹ�·ȫ��200ǧ�ף���ԭ�������ij��ȼ�����20ǧ�ף����ٹ�·ͨ����ij��;��������ʻ�ٶ������45ǧ��/ʱ���Ӽص��ҵص���ʻʱ��������һ�룮��ó�;������ԭ����������ʻ���ٶ�Ϊxǧ��/ʱ���������⣬���з�����ȷ���ǣ�������
A��
 B��
B��

C��
 D��
D��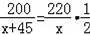

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ�� ֱ������ϵ��ABC�Ķ�����ڸ���ϣ���C������Ϊ��4��-1����
��1����������ABC��CΪ��ת���ģ���˳ʱ�뷽����ת90����ͼ�Ρ�A1B1C��
��2����ԭ��OΪ�Գ����ģ��ٻ������ABC����ԭ��O�ԳƵġ�A2B2C2����д����C2������ ____��


�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com