
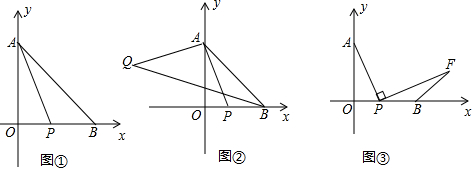
分析 (1)利用非负性求出a,b,c的值,即可OA,OB,OP,PB即可得出结论;
(2)先利用同角的余角相等得出∠AQE=∠PAO,进而判断出△AQE≌△PAO,即可判断出AE=OP,QE=OA=OB,继而判断出△MEQ≌△MOB,即可得出OM=$\frac{1}{2}$OE,即可得出结论;
(3)作出辅助线得出∠PAE+∠APE=45°,进而判断出∠APE=∠F,再用同角的余角相等判断出∠PAO=∠FPB,进而得出,△APE≌△PFB,得出AP=PF,即可得出结论.
解答 解:(1)△AOB是等腰直角三角形,
理由:∵$\sqrt{a-2}$+$\sqrt{b-2}$+(a-$\sqrt{2}$c)2=0,
∴a-2=0,b-2=0,a-$\sqrt{2}$c=0,
∴a=2,b=2,c=$\sqrt{2}$,
∴A(0,2),B(2,0),P($\sqrt{2}$,0),
∴OA=2,OB=2,OP=$\sqrt{2}$,
∴OA=OB,BP=OB-OP=2-$\sqrt{2}$,
在△AOB中,∠AOB=90°,OA=OB,
∴△AOB是等腰直角三角形,
∵BP=2-$\sqrt{2}$,OP=$\sqrt{2}$,
∴$\frac{BP}{OP}$=$\frac{2-\sqrt{2}}{\sqrt{2}}$=$\sqrt{2}$-1;
(2)如图②,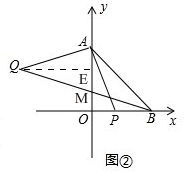 过点Q作QE⊥OA于E,
过点Q作QE⊥OA于E,
∴∠AQE+∠QAE=90°,
∵AQ⊥AP,
∴∠PAQ=90°,
∴∠QAE+∠PAO=90°,
∴∠AQE=∠PAO,
在△AQE和△PAO中,$\left\{\begin{array}{l}{∠AEQ=∠POA=90°}\\{∠AQE=∠PAO}\\{AQ=AP}\end{array}\right.$,
∴△AQE≌△PAO(AAS),
∴QE=OA=OB=2,AE=OP=$\sqrt{2}$,
∴OE=OA-AE=2-$\sqrt{2}$,
在△MEQ和△MOB中,$\left\{\begin{array}{l}{∠EMQ=∠OMB(对顶角相等)}\\{∠MEQ=∠MOP=90°}\\{QE=OB}\end{array}\right.$,
∴△MEQ≌△MOB(AAS),
∴ME=OM=$\frac{1}{2}$OE=$\frac{2-\sqrt{2}}{2}$=$\sqrt{2}$-1,
∵OP=$\sqrt{2}$,
∴$\frac{OM}{OP}=\frac{\sqrt{2}-1}{\sqrt{2}}$=$\frac{2-\sqrt{2}}{2}$;
(3)如图③,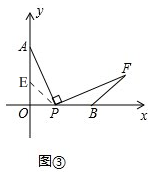 在OA上取一点E,使OE=OP,
在OA上取一点E,使OE=OP,
∵OA=OB,∴AE=PB,∵∠POE=90°,
∴∠OEP=45°,
∴∠OAP+∠APE=45°,
∵∠OAP+∠F=45°,
∴∠APE=∠F,
∵AP⊥BF,
∴∠APO+∠FPB=90°,
∵∠APO+∠PAO=90°,
∴∠PAO=∠FPB,
在△APE和△PFB中,$\left\{\begin{array}{l}{∠APE=∠F}\\{∠PAE=∠FPB}\\{AE=PB}\end{array}\right.$,
∴△APE≌△PFB(AAS),
∴AP=PF,
∴$\frac{AP}{PF}$=1.
点评 此题三角形的综合题,主要考查了全等三角形的判定和性质,同角的余角相等,解(1)的关键是求出a,b,c,解(2)的关键是作出辅助线求出QE=OB=2,OE=2-$\sqrt{2}$,解(3)的关键是作出辅助线判断出∠APE=∠F,是一道中等难度的中考常考题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
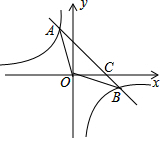 如图,一次函数y=-x+2的图象与反比例函数的图象y=$\frac{k}{x}$交于A,B两点,与x轴交于点C,已知tan∠BOC=$\frac{1}{2}$.
如图,一次函数y=-x+2的图象与反比例函数的图象y=$\frac{k}{x}$交于A,B两点,与x轴交于点C,已知tan∠BOC=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com