
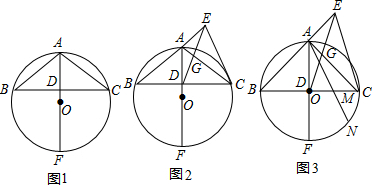
分析 (1)连接BF、CF,根据角平分线和直径所对的圆周角是直角得:∠AFB=∠AFC,则所对的弧相等,弦相等;
(2)根据等腰三角形的性质:等边对等角得:∠EDC=∠ECD,再由外角定理得:∠EGC=∠ACB+∠EDC,等量代换可得结论;
(3)作辅助线,构建高线和中位线,①证明四边形AOHE是平行四边形,得AG=GH,EG=OG=5,
②设AG=x,则GH=x,OH=2x,分别计算AG,OH,AC,AO,AM的长;
③证明△AMC∽△ACN,列比例式可求得CN的长.
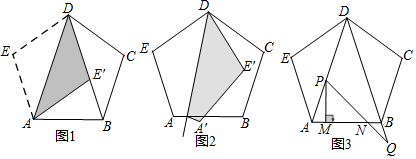
解答 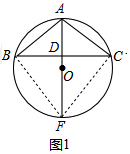 证明:(1)如图1,连接BF、CF,
证明:(1)如图1,连接BF、CF,
∵AF是⊙O的直径,
∴∠ABF=∠ACF=90°,
∵AF平分∠BAC,
∴∠BAF=∠CAF,
∴∠AFB=∠AFC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴AB=AC;
(2)如图2,∵ED=EC,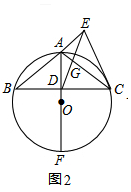
∴∠EDC=∠ECD,
∵∠EGC=∠ACB+∠EDC,
∴∠EGC=∠ACB+∠ECD=∠ACB+∠ACB+∠ECA=∠ECA+2∠ACB;
(3)如图3,连接EM,交AC于H,连接OH,
∵ED=EC,M是DC的中点,
∴EM⊥DC,
∴∠BME=90°,
∵BC为⊙O 的直径,
∴∠BAC=90°,
∵AB=AC,
∴∠B=45°,
∴△BME是等腰直角三角形,
∴∠BEM=45°,
∴△EAH是等腰直角三角形,
∴AE=AH,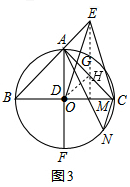
∵AB=AC,OB=OC,
∴AO⊥BC,AO=OB=OC=$\frac{1}{2}$BC,
∵∠AOC=∠HMC=90°,
∴MH∥AO,
∵M是OC的中点,
∴H是AC的中点,
∴AH=CH=OH,OH⊥AC,
∴AE=OH,
∵∠EAH=∠AHO=90°,
∴AE∥OH,
∴四边形AOHE是平行四边形,
∴AG=GH,EG=OG=5,
设AG=x,则GH=x,OH=2x,
在Rt△OGH中,52=x2+(2x)2,
x=$±\sqrt{5}$,
∴AG=GH=$\sqrt{5}$,OH=HC=2$\sqrt{5}$,AC=4$\sqrt{5}$,
∴AO=$\sqrt{A{H}^{2}+O{H}^{2}}$=$\sqrt{(2\sqrt{5})^{2}+(2\sqrt{5})^{2}}$=2$\sqrt{10}$,
∴OC=2$\sqrt{10}$,
∴MC=$\frac{1}{2}$OC=$\sqrt{10}$,
在Rt△AOM中,AM=$\sqrt{A{O}^{2}+O{M}^{2}}$=$\sqrt{(2\sqrt{10})^{2}+(\sqrt{10})^{2}}$=5$\sqrt{2}$,
∵∠N=∠B=45°,
∴∠N=∠ACB=45°,
∵∠NAC=∠MAC,
∴△AMC∽△ACN,
∴$\frac{MC}{CN}=\frac{AM}{AC}$,
∴$\frac{\sqrt{10}}{CN}=\frac{5\sqrt{2}}{4\sqrt{5}}$,
∴CN=4.
点评 本题是圆的综合题,考查了圆周角定理、等腰三角形、等腰直角三角形的性质和判定、平行四边形的性质和判定、相似三角形的性质和判定、勾股定理、弦与弧与圆周角的关系等知识,前两问比较简单,第三问较复杂,需要构建辅助线,将已知的EG进行扩散,依次利用勾股定理及边的关系求相应线段的长,并将所求线段CN放在两个相似三角形中,列比例式解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{x}$+x=1 | B. | 3x(x+1)=3 | C. | x3-3x=4 | D. | $\sqrt{x-1}$=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
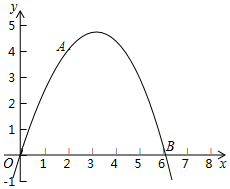 如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
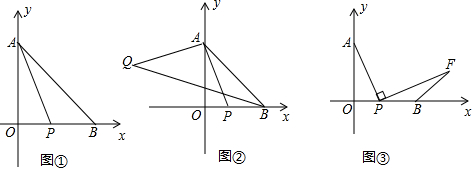
 已知一次函数y=-2x-6.
已知一次函数y=-2x-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com