
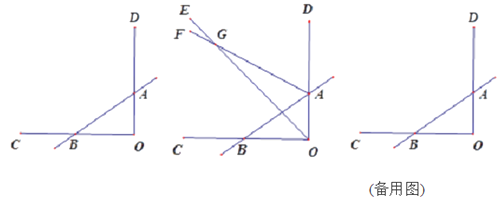
【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE与射线AF交于点G.
(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=42°,则∠OGA= ;
(2)若∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD,∠OBA=42°,则∠OGA= ;
∠BAD,∠OBA=42°,则∠OGA= ;
(3)将(2)中的“∠OBA=42°”改为“∠OBA=![]() ”,其它条件不变,求∠OGA的度数.(用含
”,其它条件不变,求∠OGA的度数.(用含![]() 的代数式表示)
的代数式表示)
(4)若OE将∠BOA分成1︰2两部分,AF平分∠BAD,∠ABO=![]() (30°<
(30°<![]() <90°) ,求∠OGA的度数.(用含
<90°) ,求∠OGA的度数.(用含![]() 的代数式表示)
的代数式表示)
【答案】(1)∠OGA=21°;
(2)∠OGA=14°;
(3)∠OGA=![]() ;
;
(4)∠OGA的度数为![]() 或
或![]()
【解析】试题分析:(1)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可;(2)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可;(3)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,根据三角形外角性质求出即可;(4)讨论:当∠EOD:∠COE=1:2时,利用∠BAD=∠ABO+∠BOA=β+90°,∠FAD=∠EOD+∠OGA得到2×30°+2∠OGA=β+90°,则∠OGA=![]() β+15°;当∠EOD:∠COE=2:1时,则∠EOD=60°,同理得∠OGA=
β+15°;当∠EOD:∠COE=2:1时,则∠EOD=60°,同理得∠OGA=![]() β-15°.
β-15°.
试题解析:(1)∵∠BOA=90°,∠OBA=42°,
∴∠BAD=∠BOA+∠ABO=132°,
∵AF平分∠BAD,OE平分∠BOA,∠BOA=90°,
∴∠GAD=![]() ∠BAD=66°,∠EOA=
∠BAD=66°,∠EOA=![]() ∠BOA=45°,
∠BOA=45°,
∴∠OGA=∠GAD∠EOA=66°45°=21°;
故答案为21°;
(2)∵∠BOA=90°,∠OBA=42°,
∴∠BAD=∠BOA+∠ABO=132°,
∵∠BOA=90°,∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD
∠BAD
∴∠GAD=44°,∠EOA=30°,
∴∠OGA=∠GAD∠EOA=44°30°=14°;
故答案为14°;
(3)∵∠BOA=90°,∠OBA=α,
∴∠BAD=∠BOA+∠ABO=90°+α,
∵∠BOA=90°,∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD
∠BAD
∴∠GAD=30°+![]() α,∠EOA=30°,
α,∠EOA=30°,
∴∠OGA=∠GAD∠EOA=![]() α,
α,
故答案为:![]() α;
α;
(4)当∠EOD:∠COE=1:2时,
则∠EOD=30°,
∵∠BAD=∠ABO+∠BOA=α+90°,
∵AF平分∠BAD,
∴∠FAD=![]() ∠BAD,
∠BAD,
∵∠FAD=∠EOD+∠OGA,
∴2×30°+2∠OGA=α+90°,
∴∠OGA=![]() α+15°;
α+15°;
当∠EOD:∠COE=2:1时,则∠EOD=60°,
同理得到∠OGA=![]() α15°,
α15°,
即∠OGA的度数为![]() α+15°或
α+15°或![]() α15°.
α15°.


科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
-5, ![]() ,0,-3.14,
,0,-3.14, ![]() ,
, ![]() ,2014,+1.99,-(-6),-2.101001000….
,2014,+1.99,-(-6),-2.101001000….
(1)正数集合:{________________________…};
(2)负数集合:{_______________________________…};
(3)非负整数集合:{________________________…};
(4)负分数集合:{_______________________…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有以下两个结论:
① 任何一个有理数和它的相反数之间至少有一个有理数;
② 如果一个有理数有倒数,则这个有理数与它的倒数之间至少有一个有理数。
则( )
A. ①,②都不对; B. ①对,②不对; C. ①,②都对; D. ①不对,②对;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四个命题:①一个多边形的内角和为900°,从这个多边形同一个顶点可画的对角线有4条;②三角形的三条高所在的直线的交点可能在三角形的内部或外部;③多边形的所有内角中最多有3个锐角;④△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形.其中真命题的是_______________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列多项式乘法,能用平方差公式进行计算的是( )
A.(x+y)(-x-y)
B.(2x+3y)(2x-3z)
C.(-a-b)(a-b)
D.(m-n)(n-m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与OD交于点F,连接DF,DC.已知OA=OB,CA=CB,DE=10,DF=6.
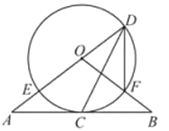
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点P(a,b)向上平移3个单位长度,再向左平移2个单位长度后得到的点的坐标是(-2,-3),那么a,b的值分别是( )
A. a=0,b=0 B. a=0,b=-6 C. a=0,b=4 D. a=5,b=-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com