
【题目】如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与OD交于点F,连接DF,DC.已知OA=OB,CA=CB,DE=10,DF=6.
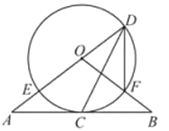
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)①连接0C,易证OC⊥AB,即可判定直线AB是⊙O的切线;②根据等腰三角形的性质可得∠AOC=∠BOC,再由圆周角定理可得![]() ,所以∠FDC=∠EDC;(2)连接EF交OC于G,连接EC,先求得EF=8,根据垂径定理得EG=FG=4,再求得OG=3,GC=2,在Rt△EGC中,根据勾股定理可得CE=
,所以∠FDC=∠EDC;(2)连接EF交OC于G,连接EC,先求得EF=8,根据垂径定理得EG=FG=4,再求得OG=3,GC=2,在Rt△EGC中,根据勾股定理可得CE=![]() ,在Rt△ECD中,再由勾股定理可得CD=
,在Rt△ECD中,再由勾股定理可得CD=![]() .
.
试题解析:(1)证明:①连接0C,
∵OA=OB,AC=BC,∴OC⊥AB.
∴直线AB是⊙O的切线.
![]()
![]()
(2)连接EF交OC于G,连接EC.
∵DE是直径,∴∠DFE=∠DCE=90°
![]()
![]()
![]()
![]()
![]()
在Rt△EGC中,CE=![]()
在Rt△ECD中,CD=![]()



科目:初中数学 来源: 题型:
【题目】为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元。2016年投入教育经费8640万元。假设该县这两年投入教育经费的年平均增长率相同。
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一根40cm的金属棒,欲将其截成x根7cm的小段和y根9cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
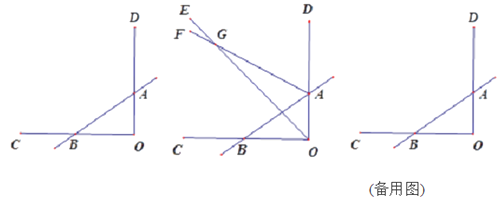
【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE与射线AF交于点G.
(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=42°,则∠OGA= ;
(2)若∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD,∠OBA=42°,则∠OGA= ;
∠BAD,∠OBA=42°,则∠OGA= ;
(3)将(2)中的“∠OBA=42°”改为“∠OBA=![]() ”,其它条件不变,求∠OGA的度数.(用含
”,其它条件不变,求∠OGA的度数.(用含![]() 的代数式表示)
的代数式表示)
(4)若OE将∠BOA分成1︰2两部分,AF平分∠BAD,∠ABO=![]() (30°<
(30°<![]() <90°) ,求∠OGA的度数.(用含
<90°) ,求∠OGA的度数.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查方式的是()
A. 调查某水库中鱼的种类
B. 调查某市市民对汽车废气污染环境的看法
C. 调查某班同学的视力情况
D. 调查某型号节能灯的使用寿命
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】其中考试后,班里有两位同学各科平均成绩相同,但是标准差不同,以下说法正确的是( )
A. 平均分数相等说明两名同学各科学习成绩一样
B. 标准差较大的说明各科成绩比较稳定
C. 标准差较大的说明成绩比较好
D. 标准差小的比标准差大的各科成绩之间差异较小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线AB上任取一点O,过点O作射线OC,OD,使∠COD=90°,当∠AOC=30°时,则∠BOD的度数是( )
A. 60° B. 120° C. 60°或90° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
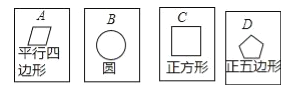
【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com