
【题目】在平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+2x+b的图象可能是( )
A.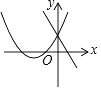
B.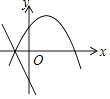
C.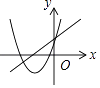
D.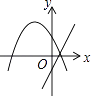
【答案】C
【解析】解:当x=0时,一次函数中y=b,二次函数中y=b,
∴一次函数与二次函数交于点(0,b),
∴B、D不正确;
∵A、C中二次函数图象开口向上,
∴a>0,
∴一次函数y=ax+b为增函数,
∴C选项正确.
故选C.
【考点精析】认真审题,首先需要了解一次函数的图象和性质(一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远),还要掌握二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】概念学习
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,例如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”,一般地,把![]() (a≠0)记作
(a≠0)记作![]() a
a![]() ,读作“a的圈n次方”.
,读作“a的圈n次方”.
初步探究
(1)直接写出计算结果:2③=________,![]() =________;
=________;
(2)关于除方,下列说法错误的是________
A.任何非零数的圈2次方都等于1; B.对于任何正整数n,1![]() =1;
=1;
C.3④=4③ ; D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
深入思考
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?

(1)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
(﹣3)④=________;5⑥=________;![]() =________.
=________.
(2)想一想:将一个非零有理数a的圈n次方写成幂的形式等于________;
(3)算一算:24÷23+(-16)×2④.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(中考·安徽)如图,已知反比例函数y=![]() 与一次函数y=k2x+b的图象交于A(1,8),B(-4,m).
与一次函数y=k2x+b的图象交于A(1,8),B(-4,m).

(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)若M(x1,y1),N(x2,y2)是反比例函数y=![]() 的图象上的两点,且x1<x2,y1<y2,指出点M,N位于哪个象限,并简要说明理由.
的图象上的两点,且x1<x2,y1<y2,指出点M,N位于哪个象限,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,BC=![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当m为何值时,关于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0.
(1)有两个不相等的实数根;
(2)有两个相等的实数根;
(3)没有实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在纸面上有一数轴,按要求折叠纸面:
(1)若折叠后数1对应的点与数﹣1对应的点重合,则此时数﹣3对应的点与数 对应的点重合;
(2)若折叠后数2对应的点与数﹣4对应的点重合,则此时数0对应的点与数对 应的点重合;若这样折叠后,数轴上有A、B两点也重合,且A、B两点之间的距离为11(点B在A点的右侧),则点A对应的数为 ,点B对应的数为 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)求证:AB=AC;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
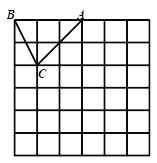
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣3.
(1)将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)与y轴的交点坐标是 , 与x轴的交点坐标是;
(3)在坐标系中利用描点法画出此抛物线.
x | … | … | |||||
y | … | … |
(4)不等式x2﹣2x﹣3>0的解集是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com