
【题目】如图,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西600的方向,从B测得小船在北偏东450的方向.
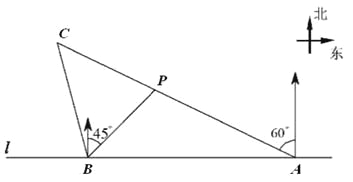
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到达点C处.此时,从B测得小船在北偏西150的方向.求点C与点B之间的距离.
(上述2小题的结果都保留根号)
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)过点P作PD⊥AB于点D,构造直角三角形BDP和PDA,PD即为点P到海岸线l的距离,应用锐角三角函数即可求解。
(2)过点B作BF⊥CA于点F,构造直角三角形ABF和BFC,应用锐角三角函数即可求解。
解:(1)如图,过点P作PD⊥AB于点D,
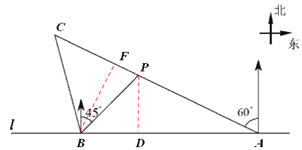
设PD=x,
由题意可知 ,PBD=45°,∠PAD=30°,
∴在Rt△BDP中,BD=PD=x
在Rt△PDA中,AD=![]() PD=
PD=![]()
∵AB=2,∴![]()
解得![]()
∴点P到海岸线l的距离为![]()
(2)如图,过点B作BF⊥CA于点F,
在Rt△ABF中,![]() ,
,
在Rt△ABC中,∠C=180°-∠BAC-∠ABC=45°,
∴在Rt△BFC中,![]()
∴点C与点B之间的距离为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18![]() m的地面上,若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是( )
m的地面上,若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是( )

A.55.5mB.54mC.19.5mD.18m
查看答案和解析>>
科目:初中数学 来源: 题型:
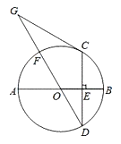
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°.
(1)求证:CG是⊙O的切线 (2)若CD=6,求GF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD=![]() ,请求出AC的长.
,请求出AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接AC,点E为正方形ABCD内一点,∠BAE=∠BCE=15°,点F为AE延长线上一点,且BF=BC,连接CF,下列结论:①EF平分∠BEC;②△BCF是等边三角形;③∠AFC=45°;④EF=AE+BE.正确的是( )
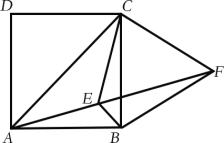
A.①②B.②③C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-2(k-1)x+k2 =0有两个实数根x1.x2.
(1)求实 数k的取值范围;
(2)若(x1+1)(x2+1)=2,试求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标![]() 中,正比例函数
中,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象经过点
的图象经过点![]() .
.

(![]() )分别求这两个函数的表达式.
)分别求这两个函数的表达式.
(![]() )将直线
)将直线![]() 向上平移
向上平移![]() 个单位长度后与
个单位长度后与![]() 轴交于点
轴交于点![]() ,与反比例函数图象在第四象限内的交点为
,与反比例函数图象在第四象限内的交点为![]() ,连接
,连接![]() 、
、![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
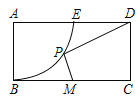
【题目】如图,矩形ABCD中,AB=2,AD=4,M点是BC的中点,A为圆心,AB为半径的圆交AD于点E.点P在弧BE上运动,则PM+![]() DP的最小值为____________.
DP的最小值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
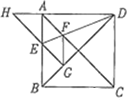
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG,则下列结论:①DE平分∠ADB;②BE=2-![]() ;③四边形AEGF是菱形;④BC+FG=1.5.其中结论正确的序号是_______.
;③四边形AEGF是菱形;④BC+FG=1.5.其中结论正确的序号是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com