
【题目】如图,在正方形ABCD中,连接AC,点E为正方形ABCD内一点,∠BAE=∠BCE=15°,点F为AE延长线上一点,且BF=BC,连接CF,下列结论:①EF平分∠BEC;②△BCF是等边三角形;③∠AFC=45°;④EF=AE+BE.正确的是( )
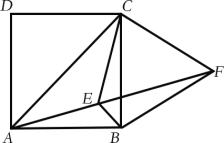
A.①②B.②③C.①②③D.①②③④
【答案】D
【解析】
利用正方形的性质,易证△ABE≌△CBE,得到∠ABE=∠CBE=45°,由三角形外角性质易得∠BEF=∠CEF=60°,所以①正确;利用BF=BC=BA,易推出∠CBF=60°,则可判定△BCF为等边三角形,所以②正确;由②的结论易得∠AFC=60°-15°=45°,所以③正确;在EF上截取FN=AE,易证△BAE≌△BFN,推出EN=BE,即可判断④.
解:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠BAC=∠BCA=45°,
∵∠BAE=∠BCE=15°
∴∠EAC=∠ECA=30°,
∴EA=EC,
在△ABE和△CBE中,
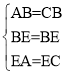
∴△ABE≌△CBE(SSS)
∴∠ABE=∠CBE=![]() ∠ABC=45°,
∠ABC=45°,
∴∠BEF=∠BAE+∠ABE=60°,
∵∠CEF=∠EAC+∠ECA=60°,
∴∠BEF=∠CEF
∴EF平分∠BEC,故①正确;
∵BF=BC=BA
∴∠BFA=∠BAF=15°,
∴∠ABF=150°,
∴∠CBF=∠ABF-∠ABC=60°,
又∵BF=BC
∴△BCF为等边三角形,故②正确;
∵△BCF为等边三角形
∴∠BFC=60°,
∴∠AFC=∠BFC-∠BFA=60°-15°=45°,故③正确;
如图所示,在EF上截取FN=AE,
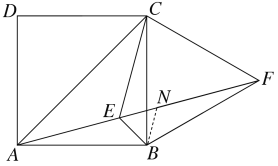
在△BAE和△BFN中,
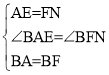
∴△BAE≌△BFN(SAS)
∴BE=BN
又∵∠BEF=60°,
∴△BEN为等边三角形,
∴EN=BE
∴EF=FN+EN=AE+BE,故④正确;
①②③④正确,故选D.


科目:初中数学 来源: 题型:
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):

(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表给出了代数式![]() 与
与![]() 的一些对应值:
的一些对应值:
| … | 0 | 1 | 2 | 3 | 4 | … |
| … | 3 |
| 3 | … |
(1)请在表内的空格中填入适当的数;
(2)设![]() ,则当
,则当![]() 取何值时,
取何值时,![]() ?
?
(3)请说明经过怎样平移函数![]() 的图象得到函数
的图象得到函数![]() 的图象.
的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块锐角三角形余料,边BC=120 mm,高AD=80mm,要把它加工成矩形零件PQMN,使矩形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.
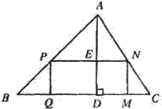
(1)当矩形的边PN=PQ时,求此时矩形零件PQMN的面积;
(2)求这个矩形零件PQMN面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE,CD交于点P,则OP的最小值是_____.
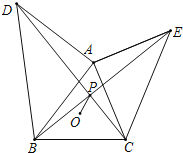
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西600的方向,从B测得小船在北偏东450的方向.
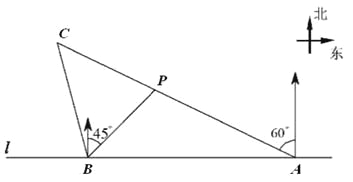
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到达点C处.此时,从B测得小船在北偏西150的方向.求点C与点B之间的距离.
(上述2小题的结果都保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
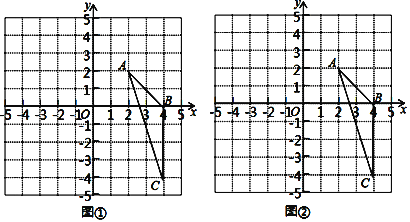
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)将△ABC绕点A顺时针旋转90°后得到△AB1C1,在图①中画出△AB1C1,并求出在旋转过程中△ABC扫过的面积;
(2)在图②中以点O为位似中心,将△ABC缩小为原来的![]() ,并写出点C的对应点的坐标.
,并写出点C的对应点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,用篱笆靠墙围成矩形花围ABCD,墙可利用的最大长度为15米,一面利用旧墙,其余三面用篱笆围成,篱笆总长为24米.
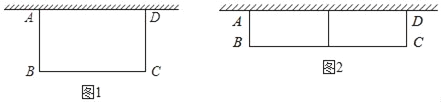
(1)若围成的花圃面积为40米2时,求BC的长;
(2)如图2若计划在花圃中间用一道隔成两个小矩形,且围成的花圃面积为50米2,请你判断能否成功围成花圃,如果能,求BC的长?如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com