
【题目】下表给出了代数式![]() 与
与![]() 的一些对应值:
的一些对应值:
| … | 0 | 1 | 2 | 3 | 4 | … |
| … | 3 |
| 3 | … |
(1)请在表内的空格中填入适当的数;
(2)设![]() ,则当
,则当![]() 取何值时,
取何值时,![]() ?
?
(3)请说明经过怎样平移函数![]() 的图象得到函数
的图象得到函数![]() 的图象.
的图象.
【答案】
【解析】
试题根据与x轴的交点坐标得到什么时候y>0.讨论两个二次函数的图象的平移问题,只需看顶点坐标是如何平移得到的即可.
(1)这个代数式属于二次函数.当x=0,y=3;x=4时,y=3.
说明此函数的对称轴为x=(0+4)÷2=2.那么![]() ,b=-4,经过(0,3),
,b=-4,经过(0,3),
∴c=3,二次函数解析式为y=x2-4x+3,
当x=1时,y=0;
当x=3时,y=0.
(2)由(1)可得二次函数与x轴的交点坐标,由于本函数开口向上,
可根据与x轴的交点来判断什么时候y>0.
当x<1或x>3时,y>0.
(3)由(1)得y=x2-4x+3,即y=(x-2)2-1.
将抛物线y=x2-4x+3先向左平移2个单位,再向上平移1个单位即得抛物线y=x2.


科目:初中数学 来源: 题型:
【题目】如图是一张长20cm、宽12cm的矩形纸板,将纸板四个角各剪去一个边长为![]() cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.
cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.

(1)这个无盖纸盒的长为 cm,宽为 cm;(用含x的式子表示)
(2)若要制成一个底面积是180m2的无盖长方体纸盒,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
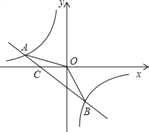
【题目】如图,已知A(–4,n),B(2,–4)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式![]() 的解集(请直接写出答案).
的解集(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
(1)现随机转动转盘一次,停止后,指针指向1的概率为 ;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
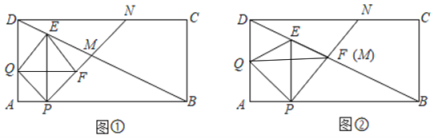
【题目】如图,矩形ABCD中,AD=4cm,AB=8cm,点P从点A出发沿![]() 边上向点
边上向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 边上向点
边上向点![]() 匀速运动,速度都是
匀速运动,速度都是![]() ,运动时间是
,运动时间是![]() ,
,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 关于
关于![]() 的对称点是
的对称点是![]() ,射线
,射线![]() 分别与
分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() .
.
(1)![]() = °;QF= ,
= °;QF= ,![]() = .(用含
= .(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 与点
与点![]() 重合时, 如图②,求
重合时, 如图②,求![]() 的值.
的值.
(3)探究:在点![]() ,
,![]() 运动过程中,
运动过程中,
①![]() 的值是否是定值?若是,请求出这个值;若不是,请说明理由.
的值是否是定值?若是,请求出这个值;若不是,请说明理由.
②![]() 为何值时,以点
为何值时,以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
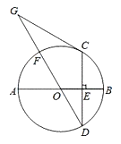
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°.
(1)求证:CG是⊙O的切线 (2)若CD=6,求GF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点A在以BC为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
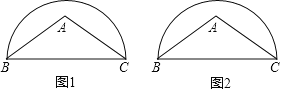
(1)在图1中作弦EF,使EF∥BC;
(2)在图2中作出圆心O.
查看答案和解析>>
科目:初中数学 来源: 题型:
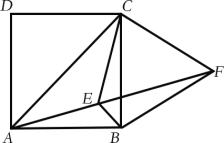
【题目】如图,在正方形ABCD中,连接AC,点E为正方形ABCD内一点,∠BAE=∠BCE=15°,点F为AE延长线上一点,且BF=BC,连接CF,下列结论:①EF平分∠BEC;②△BCF是等边三角形;③∠AFC=45°;④EF=AE+BE.正确的是( )
A.①②B.②③C.①②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com