
【题目】在平面直角坐标系中,我们把横、纵坐标均为整数的点叫做整点.已知反比例函数y=![]() (m<0)与y=x2﹣4在第四象限内围成的封闭图形(包括边界)内的整点的个数为2,则实数m的取值范围为__.
(m<0)与y=x2﹣4在第四象限内围成的封闭图形(包括边界)内的整点的个数为2,则实数m的取值范围为__.
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).

(1)在图中作出![]() 关于y轴对称的
关于y轴对称的![]() ;
;
(2)写出点![]() 的坐标(直接写答案);
的坐标(直接写答案);
(3)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),点E是线段BC的中点,分别以B,C为直角顶点的△EAB和△EDC均是等腰直角三角形,且在BC的同侧.
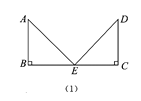
(1)AE和ED的数量关系为________,AE和ED的位置关系为________;
(2)在图(2)中,以点E为位似中心,作△EGF与△EAB位似,点H是BC所在直线上的一点,连接GH,HD,分别得到了图(2)和图(3).
①在图(2)中,点F在BE上,△EGF与△EAB的相似比是1∶2,H是EC的中点.
求证:GH=HD,GH⊥HD.
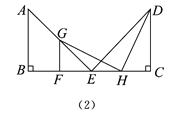
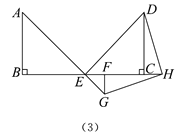
②在图(3)中,点F在BE的延长线上,△EGF与△EAB的相似比是k∶1,若BC=2,请直接写出CH的长为多少时,恰好使得GH=HD且GH⊥HD(用含k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的
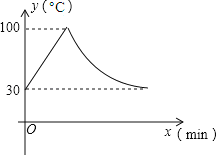
A.7:20 B.7:30 C.7:45 D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格上有6个斜三角形:
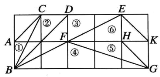
①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.
在②~⑥中,与①相似的三角形的序号是____.(把你认为正确的都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
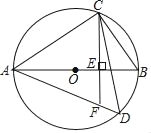
【题目】如图,AB是⊙O的直径,CE⊥AB于E,弦AD交CE延长线于点F,CF﹦AF.
(1)求证:![]() ;
;
(2)若BC=8,tan∠DAC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 正方形
正方形![]() 与等腰直角三角形
与等腰直角三角形![]() 如图
如图![]() 所示重叠在一起,其中
所示重叠在一起,其中![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() 与
与![]() 全等吗?请说明理由.
全等吗?请说明理由.
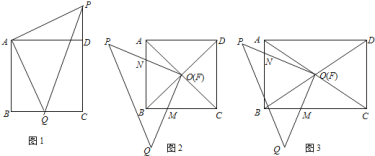
![]() 如图
如图![]() ,
,![]() 为正方形
为正方形![]() 对角线的交点,将一直角三角板
对角线的交点,将一直角三角板![]() 的直角顶点
的直角顶点![]() 与点
与点![]() 重合转动三角板使两直角边始终与
重合转动三角板使两直角边始终与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,使探索
,使探索![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
![]() 如图
如图![]() ,将
,将![]() 中的“正方形”改成“长方形”,其它的条件不变,且
中的“正方形”改成“长方形”,其它的条件不变,且![]() ,
,![]() ,
,![]() ,
,![]() ,试求
,试求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
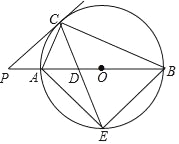
【题目】如图,AB是⊙O的直径,∠ACB的平分线交AB于点D,交⊙O于点E,过点C作⊙O的切线CP交BA的延长线于点P,连接AE.
(1)求证:PC=PD;
(2)若AC=5cm,BC=12cm,求线段AE,CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com