练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

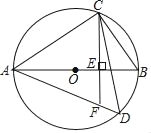
    【题目】如图，AB是⊙O的直径，CE⊥AB于E，弦AD交CE延长线于点F，CF﹦AF．

    （1）求证：；

    （2）若BC=8，tan∠DAC=，求⊙O的半径．

    【答案】（1）证明见解析；（2）8．

    【解析】

    （1）延长CF交⊙O于H，连接AH，根据垂径定理得到，根据圆周角定理证明即可；

    （2）根据直径所对的圆周角为90°，得到∠ACB=90°，根据圆周角定理得到∠B=∠DAC，根据正切的概念、勾股定理计算即可得出结论．

    （1）延长CF交⊙O于H，连接AH．

    ∵CE⊥AB，∴．

    ∵CF=AF，∴∠FAC=∠FCA，∴，∴；

    （2）∵AB是直径，∴∠ACB=90°．

    ∵，∴∠B=∠DAC，∴tanB，即，解得：AC=8，∴AB16，∴⊙O的半径为8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

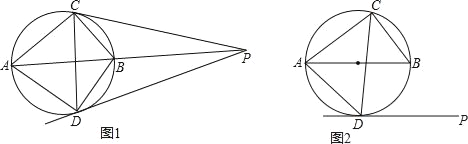
    【题目】已知⊙O的直径AB＝10，弦BC＝6，点D在⊙O上（与点C在AB两侧），过D作⊙O的切线PD．

    （1）如图①，PD与AB的延长线交于点P，连接PC，若PC与⊙O相切，求弦AD的长；

    （2）如图②，若PD∥AB，

    ①求证：CD平分∠ACB；

    ②求弦AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

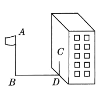
    【题目】如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21米,落在墙上的影高为6米,求旗杆的高度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

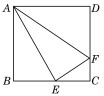
    【题目】如图，在正方形ABCD中，E是BC的中点，F是CD上一点，且CF＝CD，下列结论：①∠BAE＝30°；②△ABE∽△AEF；③AE⊥EF；④△ADF∽△ECF，其中正确的个数为(　　)

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，我们把横、纵坐标均为整数的点叫做整点．已知反比例函数y=（m＜0）与y=x2﹣4在第四象限内围成的封闭图形（包括边界）内的整点的个数为2，则实数m的取值范围为__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】Rt△ABC中，∠ACB＝90°，AC:BC＝4:3，O是BC上一点，⊙O交AB于点D，交BC延长线于点E．连接ED，交AC于点G，且AG＝AD．

    （1）求证：AB与⊙O相切；

    （2）设⊙O与AC的延长线交于点F，连接EF，若EF∥AB，且EF＝5，求BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

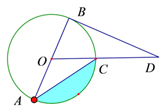
    【题目】如图，BD是⊙O的切线，B为切点，连接DO与⊙O交于点C，AB为⊙O的直径，连接CA，若∠D=30°，⊙O的半径为4.

    (1) 求∠BAC的大小；

    (2) 求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

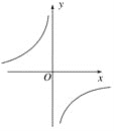
    【题目】已知函数y＝(m≠0)的图象如图所示，有以下结论：①m＜1；②在每个分支上y随x的增大而增大；③若点A(－2，a)，点B(4，b)在图象上，则a＜b；④若点P(x，y)在图象上，则点P(－x，－y)也在图象上，则下面选项正确的是( )

    A. ①②③ B. ①②④ C. ①③④ D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c的图象如图所示，对称轴为直线x=1，则下列结论正确的是（　　）

    A. ac＞0 B. 当x＞0时，y随x的增大而减小

    C. 2a﹣b=0 D. 方程ax2+bx+c=0的两根是x1=﹣1，x2=3

    查看答案和解析>>

    同步练习册答案