
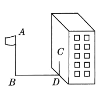
【题目】如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21米,落在墙上的影高为6米,求旗杆的高度.
科目:初中数学 来源: 题型:
【题目】如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论:
①△BDF,△CEF都是等腰三角形;
②DE=BD+CE;
③△ADE的周长为AB+AC;
④BD=CE.其中正确的是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=mx2﹣2mx﹣3m是二次函数.
(1)如果该二次函数的图象与y轴的交点为(0,3),求m的值;
(2)在给定的坐标系中画出(1)中二次函数的图象.
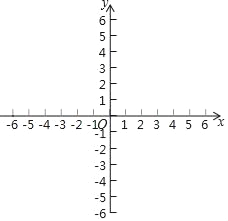
查看答案和解析>>
科目:初中数学 来源: 题型:
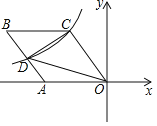
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),点E是线段BC的中点,分别以B,C为直角顶点的△EAB和△EDC均是等腰直角三角形,且在BC的同侧.
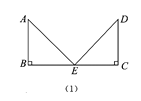
(1)AE和ED的数量关系为________,AE和ED的位置关系为________;
(2)在图(2)中,以点E为位似中心,作△EGF与△EAB位似,点H是BC所在直线上的一点,连接GH,HD,分别得到了图(2)和图(3).
①在图(2)中,点F在BE上,△EGF与△EAB的相似比是1∶2,H是EC的中点.
求证:GH=HD,GH⊥HD.
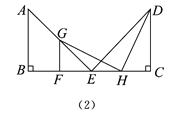
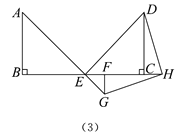
②在图(3)中,点F在BE的延长线上,△EGF与△EAB的相似比是k∶1,若BC=2,请直接写出CH的长为多少时,恰好使得GH=HD且GH⊥HD(用含k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
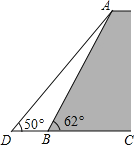
【题目】如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的
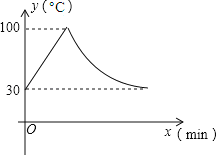
A.7:20 B.7:30 C.7:45 D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
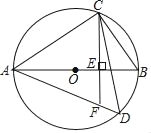
【题目】如图,AB是⊙O的直径,CE⊥AB于E,弦AD交CE延长线于点F,CF﹦AF.
(1)求证:![]() ;
;
(2)若BC=8,tan∠DAC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN.
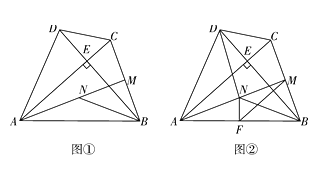
(1)求证:BN平分∠ABE;
(2)若BD=1,连结DN,当四边形DNBC为平行四边形时,求线段BC的长;
(3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com