
【题目】函数y=mx2﹣2mx﹣3m是二次函数.
(1)如果该二次函数的图象与y轴的交点为(0,3),求m的值;
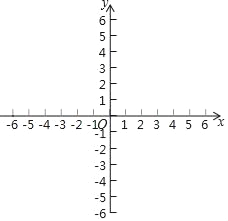
(2)在给定的坐标系中画出(1)中二次函数的图象.
【答案】(1)m=﹣1;(2)画图见解析.
【解析】
(1)由抛物线与y轴交于(0,3),将x=0,y=3代入抛物线解析式,即可求出m的值;(2)由(1)求得解析式,配方后找出顶点坐标,根据确定出的解析式列出相应的表格,由表格得出7个点的坐标,在平面直角坐标系中描出7个点,然后用平滑的曲线作出抛物线的图象.
(1)∵该函数的图象与y轴交于点(0,3),
∴把x=0,y=3代入解析式得:﹣3m=3,
解得m=﹣1;
(2)由(1)可知函数的解析式为y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点坐标为(1,4);
列表如下:
x | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 |
y | ﹣5 | 0 | 3 | 4 | 3 | 0 | ﹣5 |
描点;
画图如下:


科目:初中数学 来源: 题型:
【题目】如图1,小明将一张长为4、宽为3的矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用点F表示).
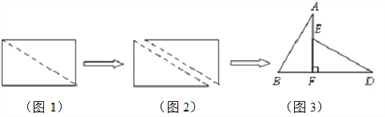
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
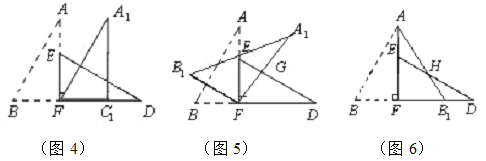
(1)将图3中的△ABF沿BD向右平移到图4中![]() 的位置,其中点B与点F 重合,请你求出平移的距离 ;
的位置,其中点B与点F 重合,请你求出平移的距离 ;
(2)在图5中若∠GFD=60°,则图3中的△ABF绕点 按 方向旋转 到图5的位置;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,试问:△AEH和△HB1D的面积大小关系.说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:

(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
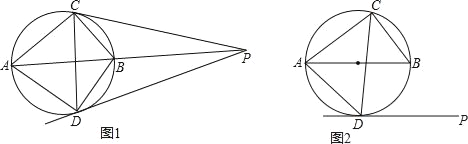
【题目】已知⊙O的直径AB=10,弦BC=6,点D在⊙O上(与点C在AB两侧),过D作⊙O的切线PD.
(1)如图①,PD与AB的延长线交于点P,连接PC,若PC与⊙O相切,求弦AD的长;
(2)如图②,若PD∥AB,
①求证:CD平分∠ACB;
②求弦AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是反比例函数y=![]() 图象上一点,PM∥x轴交y轴于点M,MP=2,点Q的坐标为(4,0),连接PO、PQ,△OPM的面积为3,求该反比例函数的表达式是△OPQ的面积.
图象上一点,PM∥x轴交y轴于点M,MP=2,点Q的坐标为(4,0),连接PO、PQ,△OPM的面积为3,求该反比例函数的表达式是△OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
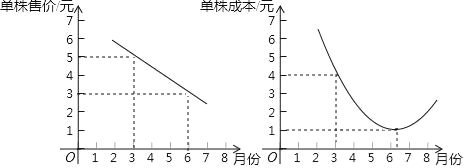
【题目】小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”.小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图表:
(1)如果在三月份出售这种植物,单株获利多少元;
(2)请你运用所学知识,帮助姑妈求出在哪个月销售这种多肉植物,单株获利最大?(提示:单株获利=单株售价﹣单株成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A、B两点,且点A的横坐标为4.
(k>0)交于A、B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线y=![]() (k>0)上一点C的纵坐标为8,求△AOC的面积.
(k>0)上一点C的纵坐标为8,求△AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
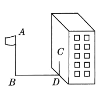
【题目】如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21米,落在墙上的影高为6米,求旗杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
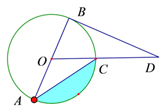
【题目】如图,BD是⊙O的切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4.
(1) 求∠BAC的大小;
(2) 求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com