
【题目】如图,P是反比例函数y=![]() 图象上一点,PM∥x轴交y轴于点M,MP=2,点Q的坐标为(4,0),连接PO、PQ,△OPM的面积为3,求该反比例函数的表达式是△OPQ的面积.
图象上一点,PM∥x轴交y轴于点M,MP=2,点Q的坐标为(4,0),连接PO、PQ,△OPM的面积为3,求该反比例函数的表达式是△OPQ的面积.
科目:初中数学 来源: 题型:
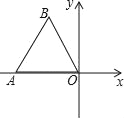
【题目】如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,则点A′的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
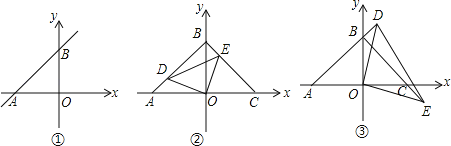
【题目】如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点,OA、OB的长度分别为a和b,且满足a2﹣2ab+b2=0.
(1)判断△AOB的形状;
(2)如图②,△COB和△AOB关于y轴对称,D点在AB上,点E在BC上,且AD=BE,试问:线段OD、OE是否存在某种确定的数量关系和位置关系?写出你的结论并证明;
(3)将(2)中∠DOE绕点O旋转,使D、E分别落在AB,BC延长线上(如图③),∠BDE与∠COE有何关系?直接说出结论,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).

(1)在图中作出![]() 关于y轴对称的
关于y轴对称的![]() ;
;
(2)写出点![]() 的坐标(直接写答案);
的坐标(直接写答案);
(3)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于![]() ,那么每套售价至少是多少元?
,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=mx2﹣2mx﹣3m是二次函数.
(1)如果该二次函数的图象与y轴的交点为(0,3),求m的值;
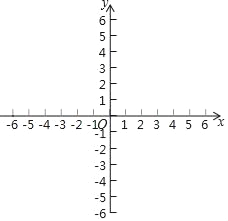
(2)在给定的坐标系中画出(1)中二次函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),点E是线段BC的中点,分别以B,C为直角顶点的△EAB和△EDC均是等腰直角三角形,且在BC的同侧.
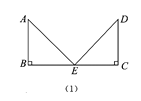
(1)AE和ED的数量关系为________,AE和ED的位置关系为________;
(2)在图(2)中,以点E为位似中心,作△EGF与△EAB位似,点H是BC所在直线上的一点,连接GH,HD,分别得到了图(2)和图(3).
①在图(2)中,点F在BE上,△EGF与△EAB的相似比是1∶2,H是EC的中点.
求证:GH=HD,GH⊥HD.
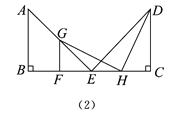
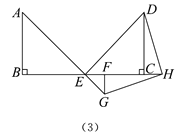
②在图(3)中,点F在BE的延长线上,△EGF与△EAB的相似比是k∶1,若BC=2,请直接写出CH的长为多少时,恰好使得GH=HD且GH⊥HD(用含k的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com