
【题目】如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点,OA、OB的长度分别为a和b,且满足a2﹣2ab+b2=0.
(1)判断△AOB的形状;
(2)如图②,△COB和△AOB关于y轴对称,D点在AB上,点E在BC上,且AD=BE,试问:线段OD、OE是否存在某种确定的数量关系和位置关系?写出你的结论并证明;
(3)将(2)中∠DOE绕点O旋转,使D、E分别落在AB,BC延长线上(如图③),∠BDE与∠COE有何关系?直接说出结论,不必说明理由.
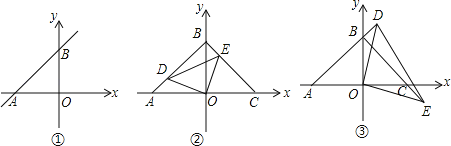
【答案】(1)△AOB为等腰直角三角形;(2)OD⊥OE;(3)∠BDE与∠COE互余.
【解析】
试题分析:(1)根据a2﹣2ab+b2=0,可得a=b,又由∠AOB=90°,所以可得出△AOB的形状;
(2)OD=OE,OD⊥OE,通过证明△OAD≌△OBE可以得证;
(3)由∠DEB+∠BEO=45°,∠ACB=∠COE+∠BEO=45°,得出∠DEB=∠COE,根据三角形外角的性质得出∠ABC=∠BDE+∠DEB=90°,从而得出∠BDE+∠COE=90°,所以∠BDE与∠COE互余.
解:(1)∵a2﹣2ab+b2=0.
∴(a﹣b)2=0,
∴a=b,
又∵∠AOB=90°,
∴△AOB为等腰直角三角形;
(2)OD=OE,OD⊥OE,理由如下:
如图 ②,∵△AOB为等腰直角三角形,
∴AB=BC,
∵BO⊥AC,
∴∠DAO=∠EBO=45°,BO=AO,
在△OAD和△OBE中,
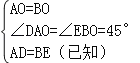 ,
,
△OAD≌△OBE(SAS),
∴OD=OE,∠AOD=∠BOE,
∵∠AOD+∠DOB=90°,
∴∠DOB+∠BOE=90°,
∴OD⊥OE;
(3)∠BDE与∠COE互余,理由如下:
如图③,∵OD=OE,OD⊥OE,
∴△DOE是等腰直角三角形,
∴∠DEO=45°,
∴∠DEB+∠BEO=45°,
∵∠ACB=∠COE+∠BEO=45°,
∴∠DEB=∠COE,
∵∠ABC=∠BDE+∠DEB=90°,
∴∠BDE+∠COE=90°
∴∠BDE与∠COE互余.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a+b=0,④b2﹣4ac>0,其中正确结论个数是( )
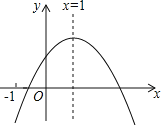
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某沿海开放城市A接到台风警报,在该市正南方向100km的B处有一台风中心,沿BC方向以20km/h的速度向D移动,已知城市A到BC的距离AD=60km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心30km的圆形区域内都将有受到台风的破坏的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?
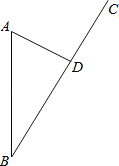
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商用8000元购进了一种衬衫,他以每件58元的价格出售,很快售完,又用17600元购进同种衬衫,数量是第一次的2倍,但每件进价比第一次多4元,服装店仍按每件58元出售,全部售完.
(1)设他第一次购进这种衬衫的价格为x元/件,则他第一次购进这种衬衫 件,他第二次购进这种衬衫 件;
(2)问他在这次服装生意中共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km.当两车均到达各自终点时,运动停止.如图是y与x之间函数关系的部分图象.
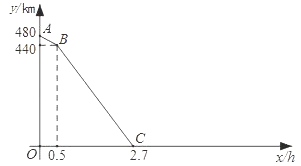
(1)由图象知,慢车的速度为 km/h,快车的速度为 km/h;
(2)请在图中补全函数图象;
(3)求当x为多少时,两车之间的距离为300km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角∠AOC和∠BOD有公共顶点O,下列结论:
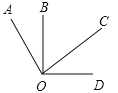
①∠AOB=∠COD;
②∠AOB+∠COD=![]() ;
;
③若OB平分∠AOC,则OC平分∠BOD;
④∠AOD的平分线与∠BOC的平分线是同一条射线,
其中正确的是 .(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
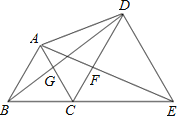
A.△ACE≌△BCD B.△BGC≌△AFC
C.△DCG≌△ECF D.△ADB≌△CEA
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com