
����Ŀ����ͼ��1������E���߶�BC���е����ֱ���B��CΪֱ�Ƕ���ġ�EAB�͡�EDC���ǵ���ֱ��������������BC��ͬ����
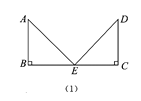
��1��AE��ED��������ϵΪ________��AE��ED��λ�ù�ϵΪ________��
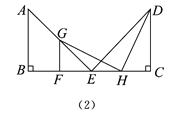
��2����ͼ��2�������Ե�EΪλ������������EGF���EABλ������H��BC����ֱ���ϵ�һ��������GH��HD���ֱ�õ���ͼ��2����ͼ��3����
����ͼ��2��������F��BE������EGF���EAB�����Ʊ���1��2��H��EC���е���
��֤��GH=HD��GH��HD��
����ͼ��3��������F��BE���ӳ���������EGF���EAB�����Ʊ���k��1����BC=2����ֱ��д��CH�ij�Ϊ����ʱ��ǡ��ʹ��GH=HD��GH��HD���ú�k�Ĵ���ʽ��ʾ����
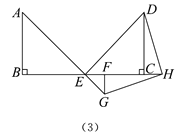
���𰸡���1��AE=ED��AE��ED����2����֤������������CH�ij�Ϊk��
��������
��1�����õ���ֱ�������ε����ʵó���ABE�ա�DCE�������ó�AE=ED��AE��ED��
��2���ٸ��ݡ�EGF���EAB�����Ʊ�1��2���ó�EH=HC=![]() EC�������ó���HGF�ա�DHC���������GH=HD��GH��HD��
EC�������ó���HGF�ա�DHC���������GH=HD��GH��HD��
�ڸ���ǡ��ʹGH=HD��GH��HDʱ���ó���GFH�ա�HCD�������ó�CH�ij���
��1���ߵ�E���߶�BC���е㣬�ֱ�BC��Ϊֱ�Ƕ���ġ�EAB�͡�EDC���ǵ��������Σ�
��BE=EC=DC=AB����B=��C=90�㣬
���ABE�ա�DCE��
��AE=DE��
��AEB=��DEC=45�㣬
���AED=90�㣬
��AE��ED��
�ʴ�Ϊ��AE=ED��AE��ED��
��2���������⣬��B=��C=90�㣬AB=BE=EC=DC��
�ߡ�EGF���EAB�����Ʊ�1��2��
���GFE=��B=90�㣬GF=![]() AB��EF=
AB��EF=![]() EB��
EB��
���GFE=��C��
��EH=HC=![]() EC��
EC��
��GF=HC��FH=FE+EH=![]() EB+
EB+![]() EC=
EC=![]() BC=EC=CD��
BC=EC=CD��
���HGF�ա�DHC��
��GH=HD����GHF=��HDC��
�ߡ�HDC+��DHC=90�㣮
���GHF+��DHC=90��
���GHD=90�㣮
��GH��HD��
�ڸ�������ó����ߵ�GH=HD��GH��HDʱ��
���FHG+��DHC=90�㣬
�ߡ�FHG+��FGH=90�㣬
���FGH=��DHC��
��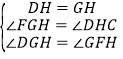 ��
��
���GFH�ա�HCD��
��CH=FG��
��EF=FG��
��EF=CH��
�ߡ�EGF���EAB�����Ʊ���k��1��BC=2��
��BE=EC=1��
��EF=k��
��CH�ij�Ϊk��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O��ֱ��AE��10cm����B����EAC����AC�ij�Ϊ��������

A. 5cm B. 5![]() cm C. 5
cm C. 5![]() cm D. 6cm
cm D. 6cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P�Ƿ���������y��![]() ͼ����һ�㣬PM��x�ύy���ڵ�M��MP��2����Q������Ϊ��4��0��������PO��PQ����OPM�����Ϊ3����÷����������ı���ʽ�ǡ�OPQ�������
ͼ����һ�㣬PM��x�ύy���ڵ�M��MP��2����Q������Ϊ��4��0��������PO��PQ����OPM�����Ϊ3����÷����������ı���ʽ�ǡ�OPQ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��![]() x��˫����y��
x��˫����y��![]() (k��0)����A��B���㣬�ҵ�A�ĺ�����Ϊ4.
(k��0)����A��B���㣬�ҵ�A�ĺ�����Ϊ4.
(1)��k��ֵ��
(2)��˫����y��![]() (k��0)��һ��C��������Ϊ8������AOC�������
(k��0)��һ��C��������Ϊ8������AOC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ֧Ԯ������ijУ���ĻС�����óO���ʽ���A��B�����ͺŵ�ѧϰ��Ʒ��1000������֪B��ѧϰ��Ʒ�ĵ��۱�A��ѧϰ��Ʒ�ĵ��۶�10Ԫ����180Ԫ����B��ѧϰ��Ʒ�ļ�������120Ԫ����A��ѧϰ��Ʒ�ļ�����ͬ��
��1����A��B����ѧϰ��Ʒ�ĵ��۸��Ƕ���Ԫ��
��2������������ѧϰ��Ʒ�ķ��ò�����28000Ԫ��������B��ѧϰ��Ʒ���ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,ijͬѧ�������˵ĸ߶�,����ijһʱ�̲��1�׳��������ֱ����ʱӰ��Ϊ1.5��,��ͬһʱ�̲�����˵�Ӱ��ʱ,����˿���һ¥��,Ӱ�Ӳ�ȫ���ڵ�����,��һ��������ǽ��,��������ڵ����ϵ�Ӱ��Ϊ21��,����ǽ�ϵ�Ӱ��Ϊ6��,����˵ĸ߶�.
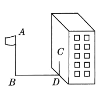
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij������BC������һ���AB���ҵ�A��B��C��ͬһ��ֱ���ϣ�С����D���۲���˶���A������Ϊ47�㣬�۲���˵ײ�B������Ϊ42����֪��D������ľ���DEΪ1.56m��EC��21m�������AB�ĸ߶Ⱥͽ�����BC�ĸ߶�(�������С����һλ)��(�ο����ݣ�tan47���1.07��tan42���0.90)
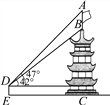
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����ǰѺᡢ�������Ϊ�����ĵ�������㣮��֪����������y=![]() ��m��0����y=x2��4�ڵ���������Χ�ɵķ��ͼ�Σ������߽磩�ڵ�����ĸ���Ϊ2����ʵ��m��ȡֵ��ΧΪ__��
��m��0����y=x2��4�ڵ���������Χ�ɵķ��ͼ�Σ������߽磩�ڵ�����ĸ���Ϊ2����ʵ��m��ȡֵ��ΧΪ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y��ax2��bx��3��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C���ҵ�C��D���������ϵ�һ�ԶԳƵ�

��1���������ߵĽ���ʽ
��2�����D�����꣬����ͼ�л���ֱ��BD
��3�����ֱ��BD��һ�κ�������ʽ��������ͼ��ش𣺵�x����ʲô����ʱ���������κ�����ֵ���ڸ�һ�κ�����ֵ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com