
【题目】如图,已知四边形ABCD为正方形,AB= ![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG. 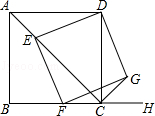
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
【答案】①证明:过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示: ∵正方形ABCD
∴∠BCD=90°,∠ECN=45°
∴∠EMC=∠ENC=∠BCD=90°
且NE=NC,
∴四边形EMCN为正方形
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中, 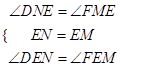 ,
,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
②解:CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°
∴∠ADE=∠CDG,
在△ADE和△CDG中,  ,
,
∴△ADE≌△CDG(SAS),
∴AE=CG
∴AC=AE+CE= ![]() AB=
AB= ![]() ×2
×2 ![]() =4,
=4,
∴CE+CG=4 是定值.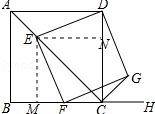
【解析】①作出辅助线,得到EN=EM,然后判断∠DEN=∠FEM,得到△DEN≌△FEM,则有DE=EF即可;②同①的方法证出△ADE≌△CDG得到CG=AE,得出CE+CG=CE+AE=AC=4即可.
【考点精析】掌握矩形的性质是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
【题目】如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C、D不重合).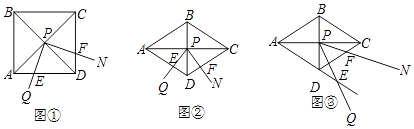
(1)如图①,当α=90°时,求证:DE+DF=AD.
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为 ![]() ,请给出证明.
,请给出证明.
(3)在(2)的条件下,将∠QPN绕点P旋转,若旋转过程中∠QPN的边PQ与边AD的延长线交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论:①∠BOE= ![]() (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论(填编号). 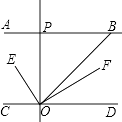
查看答案和解析>>
科目:初中数学 来源: 题型:
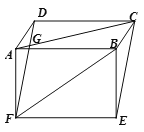
【题目】已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.
(1) 试说明DF=CE;
(2) 若AC=BF=DF,求∠ACE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接AF交对角线于点E,连接EC 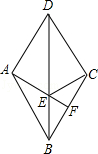
(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC的什么位置?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N. 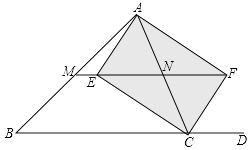
(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD和∠BDC的平分线交于E , BE交CD于点F , ∠1+∠2=90°.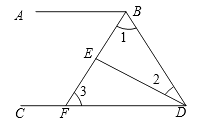
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
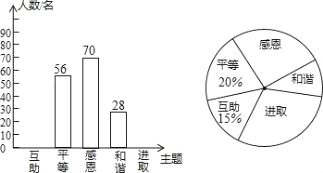
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整;
(3)计算出扇形统计图中“进取”所对应的圆心角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com