
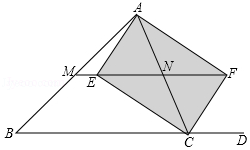
【题目】如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N. 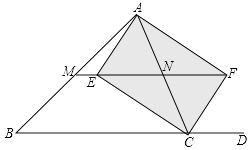
(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
【答案】
(1)证明:∵AE⊥CE于E,AF⊥CF于F,
∴∠AEC=∠AFC=90°,
又∵CE、CF分别平分∠ACB与它的邻补角∠ACD,
∴∠BCE=∠ACE,∠ACF=∠DCF,
∴∠ACE+∠ACF= ![]() (∠BCE+∠ACE+∠ACF+∠DCF)=
(∠BCE+∠ACE+∠ACF+∠DCF)= ![]() ×180°=90°,
×180°=90°,
∴三个角为直角的四边形AECF为矩形
(2)解:结论:MN∥BC且MN= ![]() BC.
BC.
证明:∵四边形AECF为矩形,
∴对角线相等且互相平分,
∴NE=NC,
∴∠NEC=∠ACE=∠BCE,
∴MN∥BC,
又∵AN=CN(矩形的对角线相等且互相平分),
∴N是AC的中点,
若M不是AB的中点,则可在AB取中点M1,连接M1N,
则M1N是△ABC的中位线,MN∥BC,
而MN∥BC,M1即为点M,
所以MN是△ABC的中位线(也可以用平行线等分线段定理,证明AM=BM)
∴MN= ![]() BC;
BC;
法二:延长MN至K,使NK=MN,
因为对角线互相平分,
所以AMCK是平行四边形,KC∥MA,KC=AM因为MN∥BC,
所以MBCK是平行四边形,MK=BC,
所以MN= ![]() BC
BC
(3)解:△ABC是直角三角形(∠ACB=90°).
理由:∵四边形AECF是矩形,
∴AC⊥EF,
∵EF∥AC,
∴AC⊥CB,
∴∠ACB=90°.即△ABC是直角三角形.
【解析】(1)证明三个角是直角即可解决问题;(2)结论:MN∥BC且MN= ![]() BC.只要证明MN是△ABC的中位线即可;(3)△ABC是直角三角形(∠ACB=90°);
BC.只要证明MN是△ABC的中位线即可;(3)△ABC是直角三角形(∠ACB=90°);
【考点精析】本题主要考查了角平分线的性质定理和菱形的性质的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某小组7位同学的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30,则这组数据的众数与中位数分别是( )
A. 30,27 B. 30,29 C. 29,30 D. 30,28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为正方形,AB= ![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG. 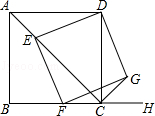
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,OA=2,AB=6点C在x轴的负半轴上,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,点D在直线AO上,点F在x轴的正半轴上,则直线DE的表达式__________________.
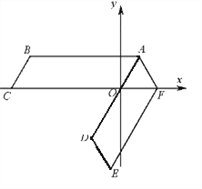
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E是ABCD中BC边的中点,若∠ABE=∠BAE=60°,BC=4,连接AE并延长交DC的延长线于点F. 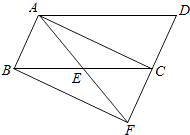
(1)连接AC,BF,求证:四边形ABFC为矩形;
(2)求四边形ABFC的周长和面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com