
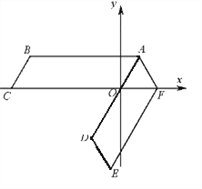
【题目】如图,四边形ABCD是平行四边形,OA=2,AB=6点C在x轴的负半轴上,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,点D在直线AO上,点F在x轴的正半轴上,则直线DE的表达式__________________.
【答案】![]()
【解析】根据旋转的性质以及平行四边形的性质得出∠BAO=∠AOF=∠AFO=∠OAF,进而求出D、E点坐标,利用待定系数法求出直线DE的表达式.
解:如图所示:过点D作DM⊥x轴于点M,
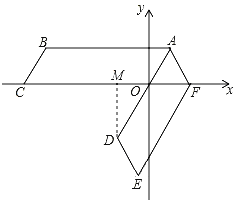
由题意可得:∠BAO=∠OAF,AO=AF,AB∥OC,
则∠BAO=∠AOF=∠AFO=∠OAF,
故∠AOF=60°=∠DOM,
∵OD=AD﹣OA=AB﹣OA=6﹣2=4,
∴MO=2,MD=2![]() ,
,
∴D(﹣2,﹣2![]() ),
),
过点E作EN⊥x轴于点N,
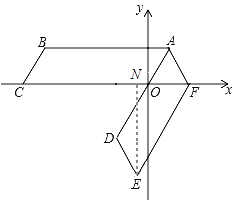
由题意可得: AD∥EF,∠AOF =60°
∴∠NFE=60°,∠NEF=30°,在Rt△ENF中,
FN=![]() EF=
EF=![]() ×6=3,
×6=3,
ON=FN﹣OF=3﹣2=1,
NE=![]() ,
,
∴E(﹣1,﹣![]() ),
),
设直线DE的表达式为y=kx+b,把D、E的坐标代入y=kx+b,得![]() .
.
“点睛”此题主要考查了平行四边形的性质以及求一次函数的解析式,正确得出D、E点坐标是解题关键.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.
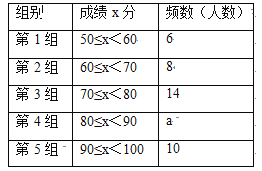
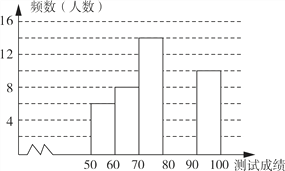
请结合图表完成下列各题:
(1)① 表中a的值为 ;
② 把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N. 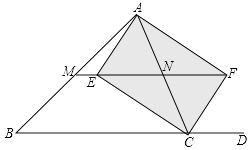
(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形的四边顺次为a、b、c、d,且满足a2+b2+c2+d2=2(ab+cd),则这个四边形一定是( )
A.平行四边形
B.两组对角分别相等的四边形
C.对角线互相垂直的四边形
D.对角线长相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解答问题:
关于勾股定理的研究有一个很重要的内容是勾股数组,在数学课本中我们已经了解到,“能够成为直角三角形三条边的三个正整数称为勾股数”,以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法:
方法1:若m为奇数(m≥3),则a=m,b=![]() (m2﹣1)和c=
(m2﹣1)和c=![]() (m2+1)是勾股数.
(m2+1)是勾股数.
方法2:若任取两个正整数m和n(m>n),则a=m2﹣n2,b=2mn,c=m2+n2是勾股数.
(1)在以上两种方法中任选一种,证明以a,b,c为边长的△ABC是直角三角形;
(2)某园林管理处要在一块绿地上植树,使之构成如下图所示的图案景观,该图案由四个全等的直角三角形组成,要求每个三角形顶点处都植一棵树,各边上相邻两棵树之间的距离均为1米,如果每个三角形最短边上都植6棵树,且每个三角形的各边长之比为5:12:13,那么这四个直角三角形的边长共需植树 棵.
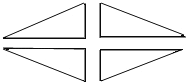
(3)某家俱市场现有大批如图所示的梯形边角余料(单位:cm),实验初中数学兴趣小组决定将其加工成等腰三角形,且方案如下:
三角形中至少有一边长为10 cm;三角形中至少有一边上的高为8 cm,
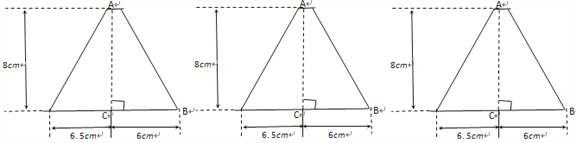
请设计出三种面积不同的方案并在图上画出分割线,求出相应图形面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com