
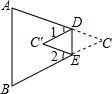
 如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=30°,求∠2的度数.
如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=30°,求∠2的度数. 分析 先根据三角形的内角和定理求出∠CEF+∠CFE=∠A+∠B,再根据折叠变换的性质,即可求出∠CEC′+∠CEC′的度数,然后利用两个平角的度数求解即可.
解答 解:如图,∵∠CEF+∠CFE+∠C=∠A+∠B+∠C,
∴∠CEF+∠CFE=∠A+∠B=75°+65°=140°,
又∵将纸片的一角折叠,使点C落在△ABC内,
∴∠C′EF+∠C′F=∠CEF+∠CFE=140°,
∴∠CEC′+∠CEC′=140°+140°=280°,
∵∠1=30°,
∴∠2=180°×2-∠CEC′+∠CEC′-∠1=360°-280°-30°=50°.
故∠2的度数为50°.
点评 本题考查了翻折变换的性质,三角形的内角和定理,熟练掌握翻折变换的性质是解题的关键.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:解答题
 如图,在一面靠墙的空地上,用长为24米的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x(m),面积为S(m2).
如图,在一面靠墙的空地上,用长为24米的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x(m),面积为S(m2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
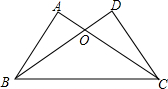 如图,已知:∠A=∠D=90°,AC=DB,求证:OB=OC.
如图,已知:∠A=∠D=90°,AC=DB,求证:OB=OC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com