
【题目】用适当的方法解下列方程
(1)x2+10x+21=0
(2)![]()
(3)![]()
(4)![]()
(5)![]()
(6)3x(x+2)=5(x+2)
(7)(3x-2)2=(x+5)2
(8)5x(x-3)-(x-3)(x+1)=0
【答案】(1)x1=-3,x2=-7;(2)x1=1+![]() ,x2=-1+
,x2=-1+![]() ;(3)x1=
;(3)x1=![]() ,x2=
,x2=![]() ;(4)
;(4)![]() ,
,![]() ;(5)
;(5)![]() ,
,![]() ;(6)
;(6)![]() ,
,![]() ;(7)
;(7)![]() ,
,![]() ;(8)
;(8)![]() ,
,![]() .
.
【解析】
(1)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
(2)利用一元二次方程的求根公式解.
(3)运用公式法求解即可;
(4)移项后发现,方程中含有公因式(x-1),因此可用提取公因式法求解;
(5)移项后发现,方程中含有公因式(x-3),因此可用提取公因式法求解;
(6)移项后发现,方程中含有公因式(x+2),因此可用提取公因式法求解;
(7)移项后,运用平方差公式进行因式分解求解即可;
(8)提取公因式(x-3)进行求解即可.
(1)x2+10x+21=0;
(x+3)(x+7)=0,
∴x+3=0,x+7=0,
∴x1=-3,x2=-7;
(2)∵a=1,b=2,c=-5,b2-4ac=24,
∴x=![]() ,
,
即x1=1+![]() ,x2=-1+
,x2=-1+![]() ;
;
(3)a=2,b=3,c=-1,
b2-4ac=9+8=17>0,
x=![]() ,
,
∴x1=![]() ,x2
,x2![]() ;
;
(4)![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() ,
,
∴![]() ,
,![]() ;
;
(5)![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() ,
,
∴![]() ,
,![]() ;
;
(6)3x(x+2)=5(x+2)
3x(x+2)-5(x+2)=0,
(x+2)(3x-5)=0
x+2=0,3x-5=0,
∴![]() ,
,![]() ;
;
(7)(3x-2)2=(x+5)2 ,
(3x-2)2-(x+5)2=0,
(3x-2+x+5)(3x-2-x-5)=0
(4x+3)(2x-7)=0
4x+3=0,2x-7=0,
∴![]() ,
,![]() ;
;
(8)5x(x-3)-(x-3)(x+1)=0
(x-3)[5x-(x+1)]=0,
(x-3)(4x-1)=0,
x-3=0,4x-1=0,
∴![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
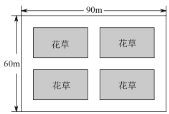
【题目】成都市中心城区“小游园,微绿地”规划已经实施,武侯区某街道有一块矩形空地进入规划试点.如图,已知该矩形空地长为![]() ,宽为
,宽为![]() ,按照规划将预留总面积为
,按照规划将预留总面积为![]() 的四个小矩形区域(阴影部分)种植花草,并在花草周围修建三条横向通道和三条纵向通道,各通道的宽度相等.
的四个小矩形区域(阴影部分)种植花草,并在花草周围修建三条横向通道和三条纵向通道,各通道的宽度相等.
(1)求各通道的宽度;
(2)现有一工程队承接了对这![]() 的区域(阴影部分)进行种植花草的绿化任务,该工程队先按照原计划进行施工,在完成了
的区域(阴影部分)进行种植花草的绿化任务,该工程队先按照原计划进行施工,在完成了![]() 的绿化任务后,将工作效率提高
的绿化任务后,将工作效率提高![]() ,结果提前
,结果提前![]() 天完成任务,求该工程队原计划每天完成多少平方米的绿化任务?
天完成任务,求该工程队原计划每天完成多少平方米的绿化任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,P为BC上的一点,连接AP,过D点作DH⊥AP于H,AB=![]() , BC=4,当△CDH为等腰三角形时,则BP=_________________.
, BC=4,当△CDH为等腰三角形时,则BP=_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决材料后的问题:
材料一:对于实数x、y,我们将x与y的“友好数”用f(x,y)表示,定义为:f(x)=![]() ,例如17与16的友好数为f(17,16)=
,例如17与16的友好数为f(17,16)=![]() =
=![]() .
.
材料二:对于实数x,用[x]表示不超过实数x的最大整数,即满足条件[x]≤x<[x]+1,例如:
[﹣1.5]=[﹣1.6]=﹣2,[0]=[0.7]=0,[2.2]=[2.7]=2,……
(1)由材料一知:x2+2与1的“友好数”可以用f(x2+2,1)表示,已知f(x2+2,1)=2,请求出x的值;
(2)已知[![]() a﹣1]=﹣3,请求出实数a的取值范围;
a﹣1]=﹣3,请求出实数a的取值范围;
(3)已知实数x、m满足条件x﹣2[x]=![]() ,且m≥2x+
,且m≥2x+![]() ,请求f(x,m2﹣
,请求f(x,m2﹣![]() m)的最小值.
m)的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
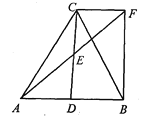
【题目】如图,在△ABC中,D是AB的中点,E是CD的中点, 过点C作CF//AB交AE的延长线于点F,连接BF.
(1) 求证:DB=CF;
(2) 如果AC=BC,试判断四边形BDCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)过点D(0,![]() )作x轴的平行线交抛物线于E,F两点,求EF的长;
)作x轴的平行线交抛物线于E,F两点,求EF的长;
(3)当y≤![]() 时,直接写出x的取值范围是 .
时,直接写出x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
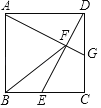
(1)证明:△ADG≌△DCE;(2)连接BF,证明:AB=FB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 中,
中,![]() 是
是![]() 中点,点
中点,点![]() 从点
从点![]() 出发沿
出发沿![]() 的路线匀速运动,到点
的路线匀速运动,到点![]() 停止,点
停止,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 路线匀速运动,
路线匀速运动,![]() 、
、![]() 两点同时出发,点
两点同时出发,点![]() 的速度是点
的速度是点![]() 速度的
速度的![]() 倍
倍![]() ,当点
,当点![]() 停止时,点
停止时,点![]() 也同时停止运动,设
也同时停止运动,设![]() 秒时,正方形
秒时,正方形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,
,![]() 关于
关于![]() 的函数关系如图2所示,则
的函数关系如图2所示,则
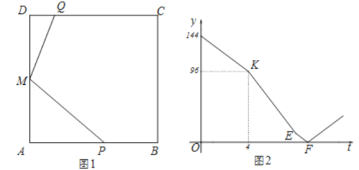
(1)求正方形边长![]() ;
;
(2)求![]() 的值;
的值;
(3)求图2中线段![]() 所在直线的解析式.
所在直线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com