
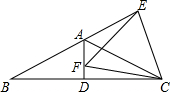
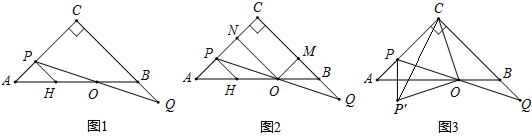
 如图,在等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点E是BA延长线上一点,点F是线段AD上一点,FE=FC.下列结论:
如图,在等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点E是BA延长线上一点,点F是线段AD上一点,FE=FC.下列结论:分析 ①连接FB,根据AD⊥BC,AB=AC,可知AD是CB中垂线,即可证明FB=FC,即可得FB=FC=FP,根据等边对等角,等量代换得到结论;
②根据三角形的内角和得到∠AEC+∠DCE+∠EBC=180°,求得∠AEC+∠DCE=150°,求得∠EFC=180°-(∠FEC+∠FCE)=60°,于是得到△EFC是等边三角形;
③首先在AC上截取AE=GA,易得△AEG是等边三角形,继而利用证得△FEA≌△CEG,即可得AC=AF+AE;
④过点C作CH⊥AB于H,易得S△ABC=$\frac{1}{2}$AB•CH,S四边形AFCE=S△ACE+S△AFC=$\frac{1}{2}$AE•CH+$\frac{1}{2}$FA•CD=$\frac{1}{2}$AE•CH+$\frac{1}{2}$FA•CH=$\frac{1}{2}$CH•(AE+FA)=$\frac{1}{2}$CH•AC,即可得S△ABC=S四边形AFCE.
解答 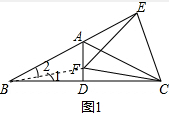 解:①如图1连接FB,
解:①如图1连接FB,
∵在等腰△ABC中AB=AC,AD⊥BC,
∴BD=CD,
∴FB=FC,
∴∠1=∠FCD,
∵FE=FC,
∴FB=FE,
∴∠2=∠FEA,
∵∠1+∠2=30°,
∴∠FCD+∠FEA=30°,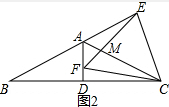 故①正确;
故①正确;
②如图2∵∠AEC+∠DCE+∠EBC=180°,
∴∠AEC+∠DCE=150°,
∵∠AEF+∠DCF=30°,
∴∠FEC+∠FCE=120°,
∴∠EFC=180°-(∠FEC+∠FCE)=60°,
∵FE=FC,
∴△EFC是等边三角形;故②正确;
③如图3在AC上截取AG=EA,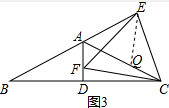
∵∠EAG=180°-∠BAC=60°,
∴△AEG是等边三角形,
∴∠EGA=∠AEG=60°,EG=EA,
∴∠AEF+∠FEG=60°,
∵∠FEG+∠CEG=∠CEF=60°,
∴∠AEF=∠CEG,
∵FE=CE,
在△OPA和△CPE中,$\left\{\begin{array}{l}{EA=EM}\\{∠AEF=∠CEM}\\{FE=CE}\end{array}\right.$,
∴△FEA≌△CEG(SAS),
∴AF=CG,
∴AC=AG+CG=AF+AE;
故③正确;
④如图4过点C作CH⊥AB于H,
∵∠PAC=∠DAC=60°,AD⊥BC,
∴CH=CD,
∴S△ABC=$\frac{1}{2}$AB•CH,S四边形AFCE=S△ACE+S△AFC=$\frac{1}{2}$AE•CH+$\frac{1}{2}$FA•CD=$\frac{1}{2}$AE•CH+$\frac{1}{2}$FA•CH=$\frac{1}{2}$CH•(AE+FA)=$\frac{1}{2}$CH•AC,
∵AB=AC,
∴S△ABC=S四边形AFCE.
故④正确.
故答案为:①②③④.
点评 此题考查了相似三角形的判定与性质、全等三角形的判定与性质、等边三角形的判定与性质、等腰三角形的性质以及三角形外接圆的知识.此题综合性很强,难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.


科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $x<-\frac{9}{4}$ | B. | $x>-\frac{9}{4}$ | C. | x>-1 | D. | x<-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com